The main aim of this paper is to illustrate by example some of the advantages of kernel density estimates (KDEs) for data presentation in archaeology. At their simplest KDEs can be thought of as an alternative to the histogram which is possibly the most commonly used statistical device in archaeology. The appearance of a histogram, and hence the archaeological inferences drawn from it, depends on both the interval width used and the starting point of the first interval. A KDE overcomes this latter defect and results in a smoother diagram that is more useful for comparative purposes. The problem of choice of interval width remains, but theory exists to guide this choice and this is discussed in the paper. Two-dimensional histograms are difficult to interpret and require large amounts of data, and KDEs offer clear advantages in this case.
After a non-technical introduction to KDEs the core of the paper is two sections on univariate and bivariate KDEs. These illustrate potential uses in archaeology and discuss some of the choices that need to be made in implementing the methodology. Some more experimental work with trivariate KDEs is also reported. Papers by the authors that deal with the more technical aspects of the methodology are electronically available.
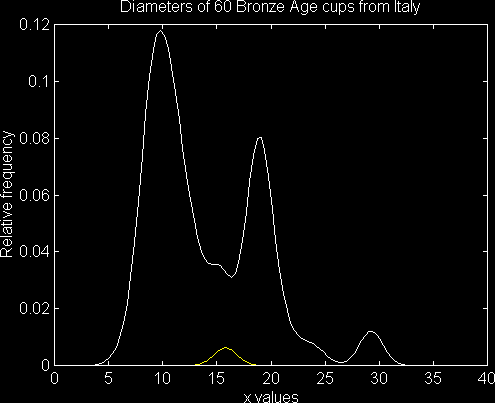
The first example illustrates how a KDE is constructed. A `bump', or kernel is centred on each data point and the heights of the bumps are summed to get the final KDE. One such kernel is shown in the plot. The final result is insensitive to the precise shape of the kernel, but does depend on its spread, or window width.

Figure 1: One dimensional KDE construction
If the spread of a kernel is allowed to vary, being wider where the points are less dense, then an adaptive kernel density estimate is obtained. This is analogous to the use of histograms with unequal interval widths. Issues concerning the choice of window-width and method will be discussed and illustrated.
Similar choices arise in the use of bivariate KDEs where, however, there is a richer choice in the way results are presented. The second example shows one possible representation of a bivariate KDE. Rotation of the figure helps to identify a suitable point for viewing the main features of the data.
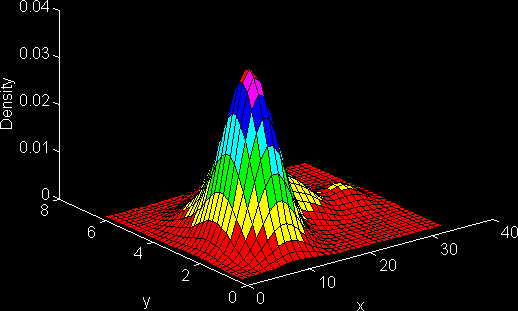
Figure 2: Two dimensional KDE, also available as an animation
The third example shows the same type of KDE, viewed from `overhead' and in the form of a contour diagram. Different approaches to contouring exist, some of which are particularly useful for identifying modes in the data, and these will be illustrated.

Figure 3: Two dimensional KDE showing contouring
That KDEs have not been much used by archaeologists may be attributable to the fact that the methodology is not yet widely available in cheap software. The examples in the paper were generated using routines written for the MATLAB package by the first author, and these will be freely available with the paper. Although MATLAB is an expensive package the much cheaper student version should be able to run many of our routines if the data sets are not too large.
Go to the table of contents
© Internet Archaeology
URL: http://intarch.ac.uk/journal/issue1/beardah/index.html
Last updated: Tue Sep 10 1996