PREVIOUS   NEXT   CONTENTS   SUMMARY   ISSUE   HOME 

Appendix 5: Chronological Modelling

Peter Marshall and Jonathan Last

June 2017

Chronological modelling has been undertaken using the program OxCal v4.2 (Bronk Ramsey 2009a; 2009b; Bronk Ramsey and Lee 2013) and the atmospheric calibration curve for the northern hemisphere published by Reimer et al. (2013). The algorithms used are defined exactly by the brackets and OxCal CQL2 keywords on the left-hand side of the technical graphs that define each model (http://c14.arch.ox.ac.uk/). The posterior density estimates output by the model are shown in black, with the unconstrained calibrated radiocarbon dates shown in outline. The other distributions correspond to aspects of the model. For example, start_earthen_long barrows is the estimated date when the earthen long barrows began to be used (Figure 15). In the text and tables, the Highest Posterior Density intervals of the posterior density estimates produced by the models are given in italics, followed by a reference to the relevant parameter name and the figures in which the model that produced it is defined.

Figure 15
Figure 15: Probability distributions of dates from earthen long barrows from southern Britain. Each distribution represents the relative probability that an event occurred at a particular time. The distributions for the start and end of the use of individual sites have been taken from the site models described in detail in Whittle et al. (2011; figs 4.7–4.13 (Hambledon Hill)), Allen et al. (2016, fig. 12a (Wor Barrow)), and Wysocki et al. (2007b, fig. 10 (Fussell's Lodge)), and are shown in outline recalculated as necessary using IntCal13 (Reimer et al. 2013). Other distributions are based on the chronological model defined here, and shown in black. For example, the distribution 'start_earthen_long_barrows' is the estimated date when the first earthen long barrow was constructed in this area. The large square brackets down the left-hand side along with the OxCal keywords define the overall model exactly

Earthen long barrows

A model for the currency of earthen long barrows in southern Britain is shown in Figure 15. This model is largely based on the data and interpretations set out by Whittle et al. (2011, fig. 14.4) and provides an estimate for the first construction of earthen long barrows in southern Britain of 3810–3660 cal BC (95% probability; start_earthen_long_barrows; Figure 15), probably 3735–3670 cal BC (68% probability). The model estimates that earthen long barrows went out of use in 3355–3055 cal BC (95% probability; end_earthen_long_barrows; Figure 15), probably 3325–3215 cal BC (68% probability).

Chambered long barrows, cairns and oval barrows

A model for the currency of chambered long barrows, cairns and oval barrows in south-central England is shown in Figures 16–19. This model is largely based on the data and interpretations set out by Whittle et al. (2011, fig. 14.41–42) and provides an estimate for the initial building of long barrows of 3760–3660 cal BC (95% probability; start_long_barrows; Figure 16), probably 3715–3605 cal BC (68% probability), and the end of their primary use of 3490–3280 cal BC (95% probability; end_long_barrows; Figure 16), probably 3460–3350 cal BC (68% probability).

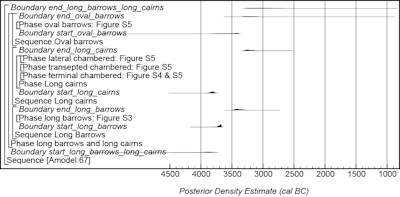
Figure 16
Figure 16: Probability distributions of dates from chambered long barrows, cairns, and oval barrows. The format is identical to that of Figure 15. The component sections of the model are shown in Figures 17–19. The large square brackets down the left-hand side along with the OxCal keywords define the overall model exactly.
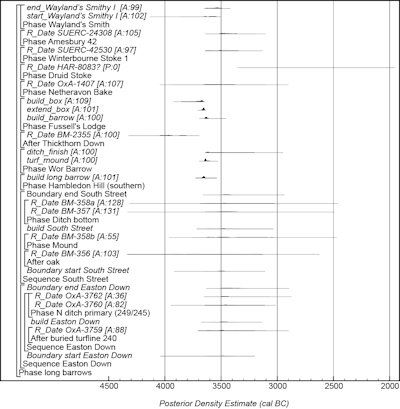
Figure 17
Figure 17: Probability distributions of dates for long barrows. The format is identical to that for Figure 15. Distributions have been taken from the site models described in detail in Whittle et al. (2011, figs 4.7–4.13 (Hambledon Hill)), Wysocki et al. (2007b, fig. 10 (Fussell's Lodge)); Bayliss et al. (2007, fig. 6 (West Kennet)), and Whittle et al. (2007, fig. 4 (Wayland's Smithy I)). The overall structure of this model is shown in Figure 16, and its other components in Figures 18 and 19.
Figure 18
Figure 18: Probability distributions of dates for chambered tombs. The format is identical to that for Figure 15. Distributions have been taken from the site models described in detail in Whittle et al. (2011; Whittle et al. (2007, fig. 4 (Wayland's Smithy I)) and Bayliss et al. (2007, fig. 6 (West Kennet)). The structure of the models for Sales Lot, Milbarrow, and Burnt Ground are derived from Whittle et al. (2011, figs 3.30, 9.25 and 9.27). The overall structure of this model is shown in Figure 16, and its other components in Figures 17 and 19.
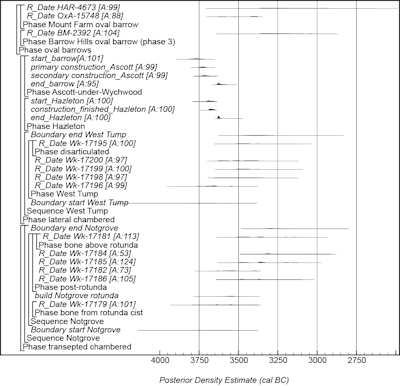
Figure 19
Figure 19: Probability distributions of dates for transepted and lateral chambered long barrows and oval barrows. The format is identical to that for Figure 15. Distributions have been taken from the site models described in detail in Meadows et al. (2007, figs 6–9 (Hazleton)), and Bayliss et al. (2007, figs 3 and 5–7 (Ascott-under-Wychwood)). The structure of the models for Notgrove, and West Tump are derived from Whittle et al. (2011, figs 9.24 and 9.26). The overall structure of this model is shown in Figure 16, and its other components in Figures 17 and 18.

Long cairns are estimated to have been first constructed in 3920–3750 cal BC (95% probability; start_long_cairns; Figure 16), probably 3855–3780 cal BC (68% probability), and their primary use to have ended in 3315–3080 cal BC (95% probability; end_long_cairns; Figure 16), probably 3290–3170 cal BC (68% probability).

Oval barrows are estimated to have been first constructed in 3850–3375 cal BC (95% probability; start_oval_barrows; Figure 16), probably 3630–3385 cal BC (68% probability), and their primary use to have ended in 3360–2905 cal BC (95% probability; end_oval_barrows; Figure 16), probably 3325–3120 cal BC (68% probability).

Linear monuments

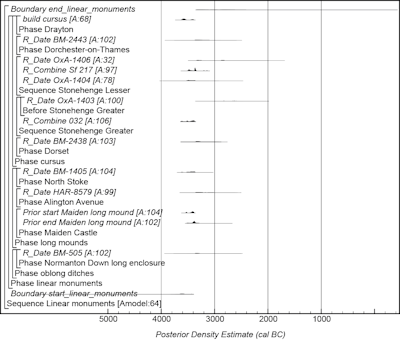
A model for the currency of linear monuments in south-central England is shown in Figure 20. This model is largely based on the data and interpretations set out by Whittle et al. (2011, fig. 14.65) and provides an estimate for the inception of linear monuments in south-central England of 3785–3395 cal BC (95% probability; start_linear_monuments; Figure 20), probably 3680–3545 cal BC (52% probability) or 3470–3410 (16% probability).

Figure 20
Figure 20: Probability distributions of dates for linear monuments. Distributions have been taken from the site models described in detail in Whittle et al. (2011, figs 4.41–4.45 (Maiden Castle) and 8.3 (Drayton)). The format is identical to that for Figure 15. The large square brackets down the left-hand side along with the OxCal keywords define the overall model exactly.

Causewayed and related enclosures

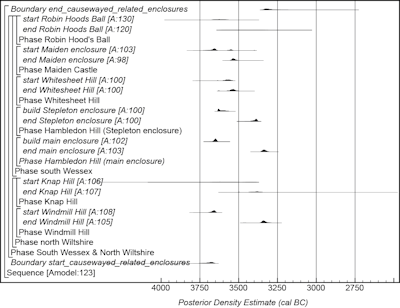
A model for the currency of causewayed and related enclosures in north Wiltshire and South Wessex is shown in Figure 21. This model is largely based on the data and interpretations set out by Whittle et al. (2011, fig. 14.2) and suggests the first causewayed and related enclosure in north Wiltshire and South Wessex was constructed in 3765–3650 cal BC (95% probability; start_causewayed_related_enclosures; Figure 21), probably 3710–3655 cal BC (68% probability). It suggests that the last enclosure in north Wiltshire and South Wessex went out of primary use in 3350–3235 cal BC (95% probability; end_ causewayed_related_enclosures; Figure 21), probably 3340–3290 cal BC (68% probability).

Figure 21
Figure 21: Probability distributions of dates for causewayed and related enclosures from south Wessex and North Wiltshire. Distributions have been taken from the site models described in detail in Whittle et al. (2011, figs 3.8–3.11; (Windmill Hill); fig. 3.25 (Knap Hill), fig. 4.51 (Robin Hood's Ball), figs 4.41–4.45 (Maiden Castle), fig. 4.26 (Whitesheet Hill), and figs 4.7–4.13 (Maiden Castle)). The format is identical to that for Figure 15. The large square brackets down the left-hand side along with the OxCal keywords define the overall model exactly.

 PREVIOUS   NEXT   CONTENTS   SUMMARY   ISSUE   HOME 

Internet Archaeology is an open access journal based in the Department of Archaeology, University of York. Except where otherwise noted, content from this work may be used under the terms of the Creative Commons Attribution 3.0 (CC BY) Unported licence, which permits unrestricted use, distribution, and reproduction in any medium, provided that attribution to the author(s), the title of the work, the Internet Archaeology journal and the relevant URL/DOI are given.

Terms and Conditions | Legal Statements | Privacy Policy | Cookies Policy | Citing Internet Archaeology

Internet Archaeology content is preserved for the long term with the Archaeology Data Service. Help sustain and support open access publication by donating to our Open Access Archaeology Fund.