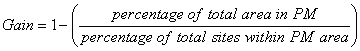
There are several ways in which a model can be evaluated, the most powerful of which is field testing of zones of low, medium and high potential. However, since field testing is beyond the scope of this project, laboratory testing is the only viable option for evaluation of the models.
Table 4: Frequencies of potential for Winnipeg study area predictive models
| % All periods | % Historic | % Woodland | % Archaic | |
|---|---|---|---|---|
| Low potential | 27.947% | 46.108% | 60.581% | 66.836% |
| Medium potential | 35.673% | 31.128% | 30.658% | 28.898% |
| High potential | 36.380% | 22.763% | 8.761% | 4.266% |
The simplest evaluation of any predictive model is by examining the relative frequencies of potential for the model. Ideally, models should have higher frequencies of low potential areas and lower frequencies of high potential areas, if the model is to be a useful management tool. It is easy to predict site locations accurately if 100% of the study area is high potential. However, this sort of model would not be advantageous if there could be no targeting of resources during survey. The results for this project and the three temporal and one traditional model are presented in Table 4 for the Winnipeg study area and Table 5 for the MbMF study area.
Table 5: Frequencies of potential for MbMF study area predictive models
| % All periods | % Paleo | % Archaic | % Woodland | |
|---|---|---|---|---|
| Low potential | 96.531% | 42.081% | 15.4707% | 68.3777% |
| Medium potential | 2.028% | 53.9912% | 81.8333% | 31.2788% |
| High potential | 1.4399% | 4.0007% | 2.6959% | 0.3435% |
For the Winnipeg study area, the traditional predictive model is actually quite poor in this case, with over one-third of the total study area being classified as high archaeological potential. As a management tool, this lessens the utility of this model. However, when looking at the temporal models, the earlier in time of the model, the more efficient it becomes as a predictor. By contrast, the MbMF models' potential frequencies match what was apparent in the visual inspection. The all-period model is a very conservative model, which has a better distribution of potential scores. Similarly the PaleoIndian and Archaic models have unacceptably large numbers of cells classified as being medium archaeological potential and insufficient numbers of cells classified as low archaeological potential. However, relative frequencies, as shown here, are a relatively crude measure of evaluation for any predictive model; as a measure, it does not reflect whether sites are being accurately predicted. In order to evaluate the predictive power of the model, other statistical evaluations are necessary.
One of the early statistical evaluation methods was proposed by Kvamme (1988), called the gain statistic. This was designed to evaluate a model's predictive power. The gain statistic allows for a comparison of percentage of sites in a percentage of land area. The gain statistic is calculated by:
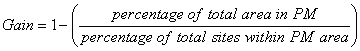
The numerator of the gain statistic comes from the percentage of the total study area which is high and medium archaeological potential for each model. This number is divided by the total number of sites in that area. The gain statistic results generally range from 0 (low predictive power) to 1 (high predictive power) (Kvamme 1988). It should be noted, however, that it is possible to calculate a gain score of -1, which means the model has reverse predictive power (it is actually better at predicting where sites are not). The results of the gain statistic for the four models are shown in Tables 6 (Winnipeg study area) and 7 (MbMF study area).
Table 6: Model evaluation gain scores (Winnipeg study area)
| Time period | Gain score |
|---|---|
| Archaic | 0.5116 |
| Woodland | 0.5268 |
| Historic | 0.4267 |
| All periods | 0.2373 |
Table 7: Model evaluation gain scores (MbMF study area)
| Time period | Gain score |
|---|---|
| PaleoIndian | 0 |
| Archaic | 0 |
| Woodland | 0 |
| All periods | 0.9476 |
At best, the models created for this project have mid- to low-levels of predictive power, with the notable exception of the all-period model for the MbMF region. For the most part, the trends shown in the relative frequencies of the distribution of archaeological potential are reinforced by the gain statistic scores. For the models for the Winnipeg study area, the traditional predictive model has a very low gain score, indicating that it has little predictive power. By comparison, the temporal models are uniformly more powerful than the traditional predictive model, but also show a trend towards more powerful models for earlier time periods. By contrast, the MbMF models are completely different. The all-period predictive model has a quite high gain statistic score, meaning that it is a fairly good predictive model. Since for all of the temporal models, all of the known site locations fall into areas of low archaeological potential, they all receive gain scores of zero, indicating they have no predictive power whatsoever.
One other early method of testing predictive models was the 'hold-back' method. In this approach a percentage of the sites in the study area were not included in the initial statistical evaluations. After the creation of the model(s), these sites were then compared against the models in order to evaluate how well the sites were predicted. I believe these methods are problematic, both generally and specifically in the case of this project. Generally, I think this approach to model testing presents difficulties in how the 'hold-back' sites are selected. First, what percentage is appropriate to hold-back in order to make the hold-back a statistically valid sample for testing? Second, how does one select these sites to ensure that the sites are not going to affect the overall statistical analysis? Specifically, in the case of this research, some of the temporal divisions are so small numerically that it would make some of the statistical analyses impractical by creating entirely too small sample sizes. Therefore, I find this evaluation method to be an unsatisfactory approach to evaluating models.
© Internet Archaeology
URL: http://intarch.ac.uk/journal/issue20/2/7.html
Last updated: Wed Aug 9 2006