1. Introduction

In 1982, US Games published the game Entombed for the Atari 2600, an early home video game console (Figure 1). Entombed was a maze game, not unusual for the time, where the player was cast into the role of an archaeologist trying to run through a dynamically generated maze while avoiding zombies, as so often happens in archaeological fieldwork. Some thirty-five years later, academic researchers reverse engineered key parts of the game's binary code, discovering a distinctive bug in the code along with an inexplicable maze-generation algorithm driven by a mysterious 32-byte table. Information from interviews filled in extant gaps in the game's development backstory and also suggested the amusing prospect that the maze algorithm was the product of intoxication. That research was written up and published by Aycock and Copplestone (2019); the story should have ended there.

However, mysteries make for compelling journalism. A freelance journalist happened across the Entombed work, and wrote a BBC Future article on it that appeared in September 2019 (Baraniak 2019), unleashing a torrent of unsolicited theories about the maze algorithm into Aycock's mailbox. About that time, we discovered recently, Entombed's algorithm got added to a 'list of unsolved problems' on Wikipedia ('List…' nd). Finally, a later, independent story for The New Yorker Radio Hour podcast in 2021 (Barron and Parkin 2021) made a critical breakthrough: they were able to contact Paul Allen Newell, something that had eluded Aycock and Copplestone. Newell was one of the two inventors of the maze algorithm, and not only had a differing account of the algorithm's creation, but also retained a number of important game-development artefacts from that time that had not previously been seen. In this article, we present and examine this new evidence to fill in the surprisingly complex development backstory that led not only to Entombed, but other games as well.

The term 'artefacts' is very deliberately chosen above, though. Through our collaboration and archaeology-based methodology, we are working under the umbrella of archaeogaming, a relatively new area of study within archaeology that Reinhard (2018a, 2) characterised as 'the archaeology both in and of digital games'. It is important to note that archaeogaming is part of the field of archaeology and draws upon its methodology; it is thus distinct from media archaeology, which 'should not be confused with archaeology as a discipline' (Huhtamo and Parikka 2011, 3). Archaeogaming topics run a broad gamut, including traditional physical excavation of video games (as occurred in New Mexico), ethics in video game research, the role of video games in heritage, and archaeology and archaeologists within games (Reinhard 2015; Flick et al. 2017; Politopoulos et al. 2019; Meyers Emery and Reinhard 2015). Here we focus on technological aspects: game implementation and game development practices. Our work with the artefacts is also interdisciplinary with computer science, affording us an informed view of the code and technology we present here.

Most notable, however, is the inclusion of Paul Allen Newell as a co-author on this article, someone who is both a first-hand participant in the historical events we describe as well as the keeper of the artefacts in question. There is precedent for this collaborative approach in archaeology, something we return to in more depth later: community archaeology, for example, is predicated on the involvement of a stakeholder community in archaeological research (Marshall 2002). In an archaeological context, this can be viewed as decolonising, allowing people the agency to tell their own stories rather than having their words and actions externally interpreted. Here, Newell provides both oral history as well as being active in performing the technical analyses. These are extremely valuable contributions, of course, but come with the potential peril of inadvertent bias in scholarship, in addition to the usual oral history pitfalls such as imperfect or selective memory (Ritchie 2015). To counter this, we maintain objectivity and critical distance in two ways. First, we clearly denote areas based on Newell's recollections — essentially information that would normally be gleaned by an interview — and label them with the initials PAN. Second, all technical analyses, regardless of the analyst, have been cross-checked by another co-author. Before we arrive at the technical solution to the mystery table's origin, however, we need to return to the story of how it came to be.

2. Less Intoxication, More Misdirection

Entombed was published by US Games, which was itself, curiously, part of the Quaker Oats Company, but the game did not originate there. Entombed, along with contemporary original and adapted games for the Atari 2600 (e.g., Towering Inferno 1982; Q*bert 1983) and other platforms, was developed at Western Technologies, where Newell was employed at the time. The maze-generation algorithm that eventually made its way into Entombed first arose as a discussion over drinks between Newell and his friend, Duncan Muirhead. Muirhead would later work for Western Technologies as well.

PAN: 'The algorithm was devised over a couple of beers at The Gas Lite on Wilshire Blvd in Santa Monica where I met Duncan Muirhead, a friend from UCLA graduate school (both of us were at UCLA 1976-1980). Duncan was a graduate student in mathematics while I was an MFA Film/TV student.
       I was working on a videogame adaptation of the movie Towering Inferno and posed the question "I need to figure out a way to have an endless number of floors with obstacles that is always passable and doesn't require me to store anything more than a subroutine to generate each floor". Duncan must have said "Oh, I know how you can do it". That led to a conversation about an endless maze that was procedurally generated that could be the source of static "floors". I have a very strong suspicion that notes on bar napkins were involved. At the end of the evening, I drove Duncan home and, over the weekend, put together the notes into a way to do it in an Atari 2600.'

While Newell was responsible for the maze algorithm's implementation in Entombed, and he and Muirhead devised the algorithm itself, the 'game' code in Entombed was written by Steve Sidley. Sidley is now a novelist; then, he was a neophyte assembly language programmer fresh out of graduate school, and just hired by Western Technologies. His recollection of events differed (Aycock 2016, 2):

'I contacted him [unclear if Newell or Muirhead] to try and understand what the maze generating algorithm did. He told me it came upon him when he was drunk and whacked out of his brain, he coded it up in assembly overnight before he passed out, but now could not for the life of him remember how the algorithm worked.'

Why the discrepancy? Newell driving Muirhead home suggests excessive intoxication was not a factor for him, but why would Sidley have been told that? Certainly it may simply have been a convenient story to dodge the question, but we argue that the answer actually lies in the ownership and perceived value of the algorithm.

PAN: 'We were young and didn't know the laws regarding IP but made the assessment that given that Duncan was not employed by WT at the time and we were on our own time when we came up with it, the actual algorithm was ours [i.e., it belonged to Muirhead and Newell].'

In fact, the artefactual record we discuss later bears this out. The maze-generation algorithm had variants used in Towering Inferno and an unreleased Atari 2600 game in addition to Entombed; Entombed sported a much-simplified version of the maze. The algorithm was thus demonstrably valuable intellectual property at the time, given its flexibility and its applicability to so many games. For the maze code Newell provided for Entombed, Sidley was only given the documentation necessary to use the algorithm: there was no documentation provided that explained how the algorithm worked. The core of the maze code was not obfuscated — a feat that would have been next to impossible, given the constraints of the Atari 2600 — but neither was it explained, until now.

3. The Muirhead-Newell Endless Maze Algorithm

It is best to begin with an explanation of the maze generation algorithm as it was reverse engineered from Entombed's binary code. This is how the algorithm was presented in Aycock and Copplestone (2019), and was the launching pad for numerous alternative theories of how the algorithm worked.

The maze as seen in Entombed (Figure 2) exhibited vertical symmetry and continuously scrolled upwards, and, as shown in the figure, it was not always possible to pass through the maze. A game mechanic called a 'make-break' acted as a workaround that permitted the player to break through inconvenient maze walls, or make new walls to thwart a pursuer or second player. A complete maze was not generated all at once, which would have demanded an amount of memory that was not available on the Atari 2600; instead, it was generated row by row on the fly as the game ran. The resulting combination of limited memory and limited compute time for maze generation necessitated an algorithm that was computationally inexpensive yet yielded good results.

As a result of the maze's symmetry, the unvarying outer wall on the left and right sides, and the use of double-wide maze passages that accommodated the player's width, each maze row was described by only eight bits. In other words, the maze generation algorithm had to select eight bits whenever a new maze row was required, where a 1 indicated a wall and a 0 a passageway, and the question was how this would be done. The bit selection could not occur in a vacuum, because at least some pathways through the maze that had been previously carved out would need to persist into a new maze row, and that meant some context had to be employed.

The algorithm used a sliding window shaped like a Tetris piece to supply context and generate its eight bits. As shown in Figure 3, two bits from the left (a and b) and three bits from above (c, d, and e) were used to produce a new bit X by using abcde to index into a table in Entombed's code, the result of which would indicate whether X should be a 0, a 1, or a bit chosen (pseudo)randomly. This process would be repeated eight times for each new maze row: starting on the left-hand side, the leftmost bit of the eight was generated, then the next to leftmost bit, and so on until finally the rightmost bit was computed. Initially, a, b, and c are always embedded in the outer wall and have no meaningful context to add yet; they are respectively assigned 1, 0, and a randomly chosen bit to start. The final position of the window has e over the line of symmetry and therefore adding the same information as d beside it, and e is instead given a random bit value there.

The logic behind how the 32-byte table mapped abcde values into X values was an open question. Why, for example, did 01101 produce 0, an empty passage, as opposed to a wall or a random selection between the two options? Aycock and Copplestone (2019, 4:11) took a conservative stance given all the available evidence, concluding that 'the table values were manually chosen, or manually tuned, by the maze algorithm designer', while others sought deeper meaning in the table (e.g., Brüning nd; colinbeveridge 2019; Mächler and Naccache 2021); it was an interesting puzzle.

The table, as it turned out, was a red herring. Note the reverse engineering performed was not incorrect, but the use of the table reflected an intermediate step rather than the algorithm's true design; there would have been no way to non-speculatively infer the actual design from what remained in Entombed. However, since Newell extensively documented the algorithm when it was developed (Figure 4), we need not speculate.

The conception of the sliding window appears flipped vertically from the Entombed version, as evident from Figure 4, although this does not affect the algorithm's operation. In fact, the original Muirhead-Newell algorithm worked bidirectionally — a feature not retained in Entombed — and a player strategy for dealing with impassable maze rows was to reverse the direction of movement, allow the offending maze rows to move offscreen, and flip movement direction again in hopes that randomness would provide a more favourable maze layout. The other major visual change is that the original algorithm did not exhibit symmetry, and needed to produce twice as many bits for new maze rows as a result.

As for the maze algorithm, the abcde context for producing an X bit is divided into three overlapping pieces, called B-KIN, D-KIN, and CBLOCK (Figure 5). Then, two values are computed based on the contents of B-KIN, both starting with the number of neighbours that share the same value as b, the tally of which can be 0, 1, or 2. B-KIN₀ takes that base value, adding 1 if b is 0; B-KIN₁ similarly adds 1 to the base value if b is 1. The same process is used to compute D-KIN₀ and D-KIN₁ for the D-KIN block with respect to d. The heart of the algorithm is the subsequent application of three rules (an example may be found in Appendix 1):

1. Any computed B-KIN or D-KIN values of 0 cause the generated X bit to be assigned accordingly to the opposite value. For instance, if B-KIN₀ is 0, then X becomes 1, and if B-KIN₁ is 0, then X becomes 0.
2. If the sum of B-KIN₀+D-KIN₀ or B-KIN₁+D-KIN₁ exceeds 4, assign X accordingly to the opposite value.
3. If the CBLOCK bits are all the same, either all 0s or all 1s, give X the opposite value.

A random bit is chosen for X for any cases not covered by the rules. Beyond the rules, though, there was one documented special case. Newell had empirically observed some undesirable mazes being generated that he isolated to the bcd bits being 010. In fact, three of the four affected cases were already handled satisfactorily by the three rules; as a result, only the single case where abcde is 00100 needs to be forced to 0. There was also an undocumented special case: in reviewing various implementations of the maze generation algorithm (discussed later) up to and including Entombed, we noticed that one case, where abcde was 11001, had been changed early on to always produce 0, yet the rationale for this modification was never captured.

We made a modern reconstruction and visualisation of the maze algorithm, providing a sandbox to experiment with the algorithm in a fashion impossible to do on an Atari 2600 (Figure 6). Because timing and code size were no longer an issue, the maze was increased to a 32x32 array to see more of the algorithm's characteristics, and this led to two observations. First, the undocumented special case of abcde=11001 prevents 'islands' of inaccessible passageways forming that are completely surrounded by walls; PAN recalls this being an issue in the early days of the maze.

Figure 6: (VIDEO) A modern reconstruction of the maze-generation algorithm, allowing experimentation. No audio.

Second, the original algorithm always calculates the next maze row from left to right, and has an observable tendency to push passages to the left where they would dead-end at the left side and increase impassibility; this observation was also made independently by 'iilaleranen' in a response to a Reddit thread (colinbeveridge 2019). Changing the algorithm to randomly decide whether the algorithm processes left-to-right or right-to-left on the row it is creating alleviates this habit. This change, plus an additional special case where abcde=00010 always yields 0 instead of a random bit, experimentally seems to improve the algorithm in terms of stability and passability.

The algorithm defies easy categorisation, and may be unique. With its reliance only on local information, it is tempting to view the algorithm as based on cellular automata (Sarkar 2000), yet the lack of parallelism and the strange shape of the 'neighbourhood' of cells surrounding X makes the cellular-automata notion contrived. The contemporaneous Eller's algorithm notably operates using maze information from only the previous maze row, and an argument has been made for why the Entombed algorithm is an adapted version of Eller's algorithm (Buck and Carter 2015; Beveridge 2019). After considering the two algorithms and consulting Eller's notes (M. Eller email to John Aycock, 23 Feb 2021), we disagree: while Eller's algorithm does indeed refer solely to information from the previous maze row, the information it acquires there effectively summarises the lineage of a passage in that row, hence it has much more to work with than the three bits Muirhead-Newell draws from the previous row.

Newell had asserted in a 2008 interview that not only were mazes generated by the Muirhead-Newell algorithm solvable, but that there was an adjustable 'difficulty control' available (Stilphen 2008). This was at odds with what was seen in Entombed. What was unseen in Entombed, however, was that the algorithm had both 'easy' and 'hard' modes — the difficulty control — and that Entombed retained only the latter. Easy mode, by contrast, produced mazes that were passable. We know that using hard mode was a deliberate design decision in Entombed, because one of the artefacts retained by Newell is a near-final printout of the Entombed source code with the easy mode code present but commented out (Figure 7). Entombed can be placed back into easy mode simply by changing two bytes in the game: specifically, change $b13b to $38, and $b140 to 3. Interestingly, other researchers had observed that the mazes would be passable given this different set of algorithm parameters (Mächler and Naccache 2021), but without the source code they could not have known the significance of this.

Beyond generating individual maze rows, Entombed contained two postprocessing checks that would identify specific, repetitive patterns in a sequence of consecutive maze rows and disrupt them. The first, which we will call PP1 for postprocessing check 1, detected an overlong vertical passage in the leftmost column, and the second (PP2) looked for excessive walls or passages in the rightmost column. Aycock and Copplestone used Entombed to generate 300,000 maze rows, and found that PP1 occurred very infrequently, only 10 times; PP2 was seen just under once per 60-row maze (Aycock and Copplestone 2019, 4:14). We duplicated their experiment with a version of Entombed that had been patched to enable easy mode, and found PP1 triggered 10,015 times in 300,000 maze rows, with PP2 used about 2.3 times as much. Our conclusion: PP1 was definitely meant to correct an easy mode flaw, and PP2's origin story is indeterminate. But we do know when they were added, thanks to an abundance of artefacts.

4. Artefacts of Game Development

Newell had saved key items capturing game development, including EPROM images, printouts, 8-inch floppy disks, and even a Polaroid picture of the maze as it existed in the middle of 1981 (Figure 8 — note that the maze is not symmetric as it is in Entombed). While many of the items were code-related, either in source code or assembled form, a variety of game design documents were also preserved. The EPROM contents were dumped, and we had the contents of the 8-inch floppies read by a professional data transfer service. For the floppies, since one by-product of data transfer was the complete raw sequence of data blocks from the disks, we wrote a program to extract the files ourselves, which we verified against the professional results; in addition, our program extracted deleted files and file fragments, where a fragment is data not associated with a file, deleted or otherwise. This left us with hundreds of artefacts, both physical and digital, as summarised in Table 1. We applied archaeological processes to keep track of this assemblage by creating a catalogue where each artefact had a unique catalogue number for reference, along with two types of metadata: objective and subjective. Objective metadata included the file/fragment name, file type (e.g., assembly source, assembler listing, hexadecimal assembler output), and provenance. An automated process marked those catalogue entries that were identical to one another for deduplication purposes. Subjective metadata consisted of analysis notes along with a catalogue entry's lineage, or classification, which we discuss shortly.

Table 1: Summary of artefacts in Entombed assemblage

Artefact Type	Count	% Frequency
Assembler listing	136	27.9
Assembly source	141	29.0
Assembly source/assembler listing	3	<1
Assembly source/document	12	2.5
BASIC program	1	<1
CP/M executable file	14	2.9
Disassembly	2	<1
Document	21	4.3
Editor backup file	80	16.4
Hex assembler output	47	9.7
Hex assembler output/assembler listing	1	<1
Hex assembler output/assembly source	1	<1
Picture	1	<1
ROM image	1	<1
Contents missing or unidentifiable	26	5.3
TOTAL	487	100

The existence of subjective metadata correctly implies that we worked through all 487 catalogue artefacts, analysing and cross-checking the analysis of each, and constructing a probable timeline/sequence for their creation based on differences in the code as well as automated and manual versioning information in the filenames. The editor that Newell used to write code would automatically create a .bak backup file of the previous state of a file that would get updated every time the file was saved. This meant that most times, the .bak files would contain very minor, even micro, changes, whereas larger changes would be reflected in Newell's manual versioning practice.

PAN: 'Once a point has been reached in the code where what one has is "good" and is significantly different from the last "good" state, there is a hesitancy to proceed ahead without capturing what is "good". The assessment of what this point should be is subjective — the point of no return once I am ready to make a new major change is a gut reaction. For example, when I had a tested one-player game and I was ready to add a second player, I created an archive backup as I knew that change would initially break the existing code.'

In modern development, changes to code would typically be tracked using a system like Git, and such revision control systems did exist for larger systems in the early 1980s (Rochkind 1975). Newell, working on smaller computer systems, employed a versioning method that is doubtless familiar to people even today: he used the filenames to reflect changes. Minor versions within a sequence of code were denoted by incrementing a letter or number at the end of the filename, like MAZT to MAZU or MINOTR5 to MINOTR6; major lines of development were assigned distinct filename 'stems', such as MAZ versus MINOTR in the previous example. From an archaeological perspective, Newell has provided a curated assemblage with excellent stratigraphy — and to understand the relationships between each version (and link them with their backups), we can approach versions as stratigraphic units.

How can digital artefacts be analysed using principles from stratigraphy? In traditional physical archaeology, the Harris matrix is a method for describing and schematically representing stratigraphy: all of the layers (e.g., sediments or strata that form in nature through geological processes), features (e.g., human-formed pits, burials, wells, walls), and interfaces (or once-exposed living surfaces that are now buried) that are present in an archaeological site (Price and Knudson 2018, 215). More specifically, the Harris matrix allows for capturing the relative sequence of these deposits in an archaeological site. Each layer, feature, and interface in a site, as interpreted from a stratigraphic profile, is given a unique identifier, then each is connected to one another using lines. This provides an overall understanding of the processes, both cultural and natural, that have shaped and created the archaeological site.

For digital artefacts and sites, we can use the overall concept of the Harris matrix, but instead of capturing the sequence of site formation we are representing the various changes and stages in game development and implementation. There is precedent for this: Reinhard (2018b) used the Harris matrix to visually represent the history and process of game development for No Man's Sky although, unlike his work, we do not have detailed or complete documentation nor patch notes for each version of the game. Through our analysis, we have grouped our artefacts into four main lineages — MAZGAM, MAZONLY, ENT, and TOW — to reflect their distinct purposes. MAZGAM is Newell's initial development sequence as he implemented the maze algorithm and created a complete, unreleased game with it that allowed 1–2 players and had 42 game variations. The maze code was spun off for use in Towering Inferno (TOW), and a separate code sequence (MAZONLY) simplified and optimised the maze code into a form that could be handed off to another programmer and was then used in Entombed (ENT).

Figure 9 shows the Harris matrix resulting from our analysis process. Following the principles of stratigraphy, the oldest artefacts are positioned on the bottom of the matrix. Dashed lines indicate development offshoots that were off the 'main' MAZGAM–MAZONLY–ENT line leading to Entombed that we are focusing on here. Both MAZGAM and MAZONLY had multiple versions that are shown expanded out in Figure 9. This illustrates a relative sequence of artefacts, for which Newell's versioning helped tremendously, but our analysis also involved understanding the code changes between the different versions. In cases where the assembly source code was complete, we assembled the code using a modern assembler and ran it in-emulator to see the behaviour and appearance of the different versions too. Placing the artefacts precisely in time was trickier, though. Archaeologists, like historians, must be cautious when an artefact has a calendar date as one of its attributes. There are several reasons why a recorded date still requires interpretation, including curatorial effects (e.g., people retain, reuse, and/or recycle things), and challenges around interpreting what a recorded date means (e.g., a date on a plate commemorating an important event represents the event, not the date of manufacture, design, or production). We also have to consider that many smaller computer systems of this era did not have real-time clocks, and people failing to set the date and time manually on their computers could make file timestamps misleading. This means that artefacts with calendar dates are useful as a starting point but all require thoughtful critique and comparison with other artefacts in the assemblage before being used as definitive anchors for our Harris matrix.

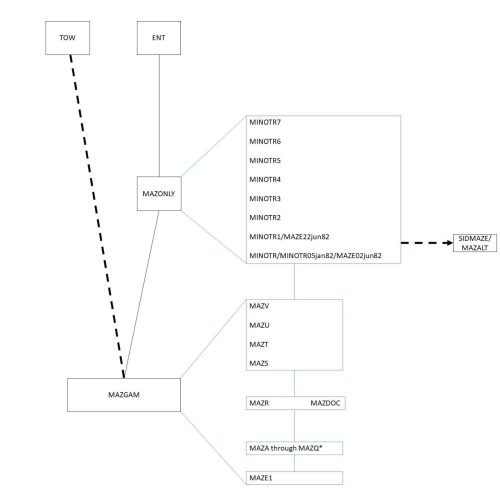
The dates associated with some of the artefacts did provide a good starting point, both artefacts that were part of the development sequence as well as those that were co-located in the same context. For example, some files recovered from a specific floppy disk contain dates that fall within August 1981, which aligns with Newell's timeline for when the maze game was being worked on; PAN recalls the 'beer meeting' with Muirhead was in July or early August 1981. The earliest full date found on any artefact within our assemblage is August 12, 1981, found in CITY3.ASM, and LOAD3.DOC has the date of August 21, 1981. (Some CP/M system files on the floppy disks do bear earlier dates, but none of these are related specifically to game development and they have been excluded from our catalogue and analysis.) These two artefacts are associated with the maze game through their context on the disk, but neither belongs to the development sequence represented by the Harris matrix. The first dated maze game artefact we have a listing for is August 1981, and logically the code would have been developed prior to the time of that listing. This artefact, MAZDOC.ASM, exemplifies a number of interpretation challenges and warrants closer examination.

MAZDOC.ASM was one of a very few extensively documented versions of source code; such documentation is very important in capturing a programmer's process and decisions, i.e., the technological choices made. Newell's typical practice at that time tended towards few comments in the versions of the code being actively developed, compensating periodically by thoroughly documenting selected milestone versions. The MAZDOC file recovered from disk contains the date August 28, 1981, and this is a critical artefact for establishing our sequence because it has an early date and it is clearly an early version of the maze code that would be reworked and refined into Entombed. Even here there is some dating ambiguity, however, as the corresponding printout of MAZDOC has the '28' scratched out. That aside, comments in the file say that 'IT HAS ANCESTORS STORED ON MANY APPLES DISKS, A EARLIER VERSION CALLED MAZE1 WHICH HAS ONLY ONE OBJECT'. This is an obvious smoking gun — it tells us that MAZDOC isn't the oldest artefact in the assemblage nor does it represent the earliest artefact in the maze game implementation. This was affirmed by code analysis: among other changes, there is a bug fix from MAZE1 to MAZDOC. The 'APPLE' mention reflects initial development at Western Technologies using Apple II systems, later shifting to Ithaca InterSystems CP/M-based computers and their 8-inch disks. Unfortunately, while we have MAZE1, the (5¼-inch) Apple disks and their contents are not in the assemblage, and that raises other questions.

Despite the reference to 'ANCESTORS,' we have found no explicit mentions of any versions preceding MAZR except for MAZE1. Did they exist? One theory is that they did not: 'E' and 'R' are adjacent on a QWERTY keyboard, and transforming 'MAZE' into 'MAZR' would be an easy typo to make; perhaps 'MAZR' occurred by happenstance and Newell whimsically carried on the naming with MAZS. PAN strongly disagrees: an alternate theory has him starting with the 'MAZ' stem at MAZA or MAZE and using consecutive letters, which would leave either 17 or 13 versions missing, respectively. With several backups a week, these numbers seem plausible, and they are consistent with evidence of frequent letter-based backups appearing in the TOW lineage. On the balance of probabilities we would side with the missing-versions theory, but we have marked the absent versions with an asterisk in the Harris matrix to indicate the uncertainty. Similarly, there is some debate over the relative ordering of MAZR and MAZDOC, and we have shown them as contemporaneous in Figure 9 for this reason.

MAZGAM is a particularly interesting lineage, because it encapsulates the development of a game from beginning to end. MAZE1, the earliest version with no gameplay per se, has a single player navigating a maze, where the player representation is a simple square. By the time of MAZR/MAZDOC, the square has multiplied: there are two players who must traverse the maze in a cooperative manner, owing to the fact that both player squares must always be on-screen. MAZS marks changes not in gameplay but in appearance, with the maze rendered in a more stylised fashion (a look that did not persist beyond MINOTR1), and extensive code changes to refine the player representation to reflect the direction of movement and remove flickering.

MAZT has only minor internal changes, but the same cannot be said of MAZU, which introduces the ability for players to create walls by pressing the joystick's fire button, the start of what would eventually become the make-break in Entombed. Finally, MAZV is the culmination of the game's development, opening with Newell's initials and a logo, and permitting one of 42 variants to be selected. Multiple game variants were not uncommon for Atari 2600 games — for example, Combat (1977) was the 2600's earliest pack-in game, and sported 27 variations — and the challenge for the programmer was to implement them all using the constrained amount of space available. Among the variants in MAZV, one of the most involved was a two-player 'cat-and-mouse' game, with the players' ability to make or break maze walls fully fleshed out. Figure 10 shows this variant being played. While space precludes a detailed, version-by-version description of all the changes made in the MAZGAM code sequence, it is worth noting that the code versions show increasing sophistication, both in terms of the assembly language programming generally and the use of the Atari 2600 specifically, a trend that continues into the MAZONLY sequence.

Figure 10: (VIDEO) Gameplay of the unreleased Atari 2600 game. No audio.

Newell was an employee of Western Technologies from June 1981 to shortly after his Vectrex game, Scramble, was finished in April 1982. He then worked as a consultant to finish Towering Inferno and package up the minimal maze code for Steve Sidley to use in Entombed. PAN admits that his approach as a consultant in 1982 was from a very different mindset than when he first thought of a maze game back in 1981. Using the artefacts, we can track this shift in his thinking where in the beginning the MAZGAM versions were focused on making the concept work as a game, whereas the MAZONLY versions that would be given to Sidley are akin to the demolition contractors do prior to a remodel — all of the 'extras' are stripped away, leaving only the structure and working parts. The start of the MAZONLY sequence, MINOTR, begins where MAZV left off, and we place it later owing to MINOTR's code fixing some bugs in MAZV. To walk through the remainder of the MAZONLY sequence, we will use three key elements of the maze algorithm as a lens.

Mystery table. The mysterious 32-byte table, called NEWT in the source code, makes its debut in MINOTR3. At first, a simple encoding is used; it is only in MINOTR6 that the table takes its more cryptic but efficiently encoded final form that carries through to Entombed. All versions prior to MINOTR3 map the five abcde bits into X values using a cascade of conditional tests, comparing abcde to different values one by one to apply the Muirhead-Newell algorithm's rules and special cases. The NEWT table encapsulates the result of this previous code in a more efficient manner. In one of the file fragments we recovered from the disk images, there was an interesting evolutionary step, where both the NEWT table along with the code the table replaced were temporarily co-existing, underscoring the importance of not limiting data recovery to the files listed in the floppy disk directories.

Easy mode. Easy mode initially manifests itself in MINOTR4, which is hardwired to always be in that mode, making the generated mazes passable. The two different modes are enshrined in the code in MINOTR7 (Figure 11), which effectively acted as a maze-generation demo program to give to Sidley; the Atari 2600's 'color/b∙w' switch was used to change between the two modes as the demo ran. MINOTR7 is also the genesis of the Entombed code excerpt shown in Figure 7.

Figure 11: (VIDEO) MINOTR7's maze-generation demo in operation. No audio.

Postprocessing. A preliminary form of PP1 appeared as far back as MINOTR3, suggesting that Newell was already aware of the need to break up certain undesirable maze formations at that time. Some experimentation is evident, as a value controlling PP1's behaviour that was introduced in MINOTR3 changes in MINOTR5, and again in MINOTR6, where it takes on the value seen in Entombed. PP2 shows up later than PP1, in MINOTR5, with subsequent adjustment in MINOTR6.

Documentation of the MAZONLY series in preparation for transferring the maze code to Sidley did not begin in earnest until MINOTR7, and comparison with the editor backup MINOTR7.BAK shows that the final change was the addition of a large explanatory comment at the start of the file. There were other finds in the assemblage, such as a fledgling attempt at an alternative maze algorithm extracted from file fragments (MAZALT, probably written by someone other than Newell), but the highlight of the non-code artefacts was a set of four game design documents.

The earliest design document, dated October 1981, describes the unpublished game Minotaur, which in our Harris matrix is the end result of the MAZGAM and the start of the MAZONLY sequences; the game's name and the October date coincide with those found in the documented code. Even here the archaeological record is ambiguous; there is a physical test cartridge whose label mock-up shows the unpublished maze game bearing the name Amaze, Newell's working title at the time. Minotaur is credited to Newell with the maze algorithm credits including both Muirhead and Newell. This design document — the only one PAN had a direct hand in writing — is followed by an undated, uncredited one simply called Maze. An ambitious design centred around mazes; each Maze level had two 'phases', a scrolling maze followed by a static maze, ultimately trying to collect 'treasure' while avoiding computer-controlled 'uglies'. The make-break of Entombed features in Maze's design, although as mentioned the concept can be traced back to Minotaur.

The final two design documents reflect a more formalised approach to game design, not completely free-form documents but each a structured form with defined sections to fill in. Since determining accurate game credits for Entombed was a particular challenge (Aycock and Copplestone 2019, 4:17), Figure 12 includes the headers for both files. Sidley was clearly at Western Technologies by that time in July 1982, and others have entered the picture as well. The Maze Chase document is really the Maze design fleshed out in slightly more detail, but a significant change in design occurred over the next few weeks. By that time, Maze Chase had become Zoomie Zombie, the two-phase idea had been abandoned, the uglies were zombies, and the player character was an archaeologist. Apart from a few minor details, the Zoomie Zombie design is easily recognisable as Entombed. A plaque produced to commemorate Entombed credits, in order, Steve Sidley, Paul Newell, Tom Sloper, and Duncan Muirhead.

5. Discussion

This article expands the boundaries of archaeogaming — it is touching upon autoethnography because one of the main figures behind the game, who produced and curated the artefacts we examined, is a co-author. Autoethnography is a reflexive form of qualitative research where the author describes and analyses personal experiences to understand their broader cultural context (Ellis et al. 2010). It has seen occasional use in recent archaeogaming work, such as Smith Nicholls' (2021) examination of mapping video games, and Graham's (2020) expedition into Minecraft used as a vehicle to explore ethics. Incorporating this approach into archaeogaming highlights some of the issues in archaeologies of the contemporary, ethnoarchaeology, and anthropology more broadly, including: How do we include living people in research? What are the benefits and limitations of working with informed informants? How do we account for bias and the curation and censoring of technological knowledge? How do we validate and legitimise voices or scholarship? Who owns not just the artefacts we study but the information and interpretations we generate? Some of these we have already addressed through our research methodology, and in this section we consider the remainder.

Co-authorship is a traditional means of inclusion within academic publication, a pattern we both follow and challenge here. Gottlieb (1995) discusses the challenges and trials of anthropological writing; these include how the voices of informants/participants, assistants, and even spouses are merged into a singular academic one through the use of the impersonal first-person plural, and how individual contributions and analytical or interpretative disagreements are rarely well represented in co-authored works. Graber (2010) reflects upon the practice of including 'personal communications' as one example of the uncertainties anthropologists (and specifically graduate students) face as they navigate academic professionalisation and challenge conceptualisations of ownership of ideas and discourses while 'necessarily excluding other ways of thinking about intellectual origin and attribution'. While we have merged our voices in this article, we also wanted to ensure that Newell's voice, perspective, and contributions are presented clearly throughout. This led to our decision, after some debate, to use PAN for his recollections or 'personal communications'.

Kumar (2018) concludes that while steps have been taken to formalise co-authorship, largely via Codes of Conduct and in instructions for authors, the underlying ethical challenges of what co-authorship represents, what value it brings to publication integrity, what it means to the participating authors versus other forms of acknowledging contribution, remain. As demonstrated throughout, having Newell as a formal co-author and an active participant in shaping the research and writing process has been valuable in terms of addressing outstanding questions about Entombed, but also became an outlet for Newell to engage in a meaningful way and process and reflect upon his role in shaping Entombed. There is precedent: Lee et al. (2019) is an example of inclusion of a research informant as a co-author intentionally to highlight the colonial and exclusionary practices of archaeology and palaeoanthropology in Africa, while arguing for the inclusion of Indigenous/local ontologies and epistemologies in all aspects of research taking place in and about their homelands. Mickel (2021) expands upon these critiques and challenges in acknowledgement and recognition of labour in archaeology, illustrating the expertise and 'nuanced' knowledge about archaeology and the past that 'unskilled', local community members hired to excavate sites have. Throughout our work, Aycock and Biittner have included Newell intentionally and holistically, and we have centred his labour in two ways. First, in the form of his work and contributions to Entombed (Newell as programmer, Newell as interlocutor); second, in the narrative we have produced here (Newell as research collaborator, Newell as co-author).

However, in our efforts to foreground Newell and his work, it would be remiss of us to overlook the fact that the other two co-authors will necessarily bring their own biases to the work. The interdisciplinary perspectives, with Aycock from computer science and Biittner from anthropology and archaeology, add immense value in that they give us the ability to understand digital artefacts and frame them in the context of human activity. Yet while we have strived to maintain objectivity relative to the inherently subjective recollections Newell provided, by cross-checking technical analyses and clearly denoting the distinction with 'PAN', ultimately there are limitations. Even technical analyses involve interpretation and, for example, the alternative theories surrounding the missing versions of the maze code led to a difference of opinion that was resolute enough to be noted above.

Although questions relating to co-authorship and acknowledgement are not new to anthropology, ethnography, archaeology, or any field involving living humans or participatory-based research, they do pose specific, unique challenges in the archaeogaming context. This is because with digital games we have not just the context of production/implementation, which is our focus, but also the context of use (e.g., gameplay and community building in gaming communities) and the context of how users/players are active participants in creating histories of game development, design, and implementation. Admittedly this research is somewhat unique in that we have a research collaborator who is the original programmer, who is also the individual who curated the archaeological record that we are analysing, and can provide insights into the curatorial process. As rare as this situation might be, it results in a situation that is familiar to any researcher engaged in ethnography, that of change over time. As Margaret Mead (2001) reflects upon in subsequent prologues to her famous 1928 book Coming of Age in Samoa, both the anthropologist and their informants/participants change over time — how we understand the world and ourselves in our youth is unlikely to remain the same as we mature and age. Further, our recollections of events in our past become obfuscated, not only through the process of ageing that includes memory decay/loss, but also because we are able to recontextualise and to reflect upon ourselves and the change(s) we've experienced, which is the key to autoethnography.

One of the other issues that arose out of Aycock and Copplestone's (2019) work was highlighting the conflict that can arise when researchers publish interpretations that are inconsistent with those of the community members. The inadvertent crowdsourcing of Entombed's 'mystery table' origins led to many an alternate theory making its way into Aycock's mailbox, an unexpected windfall that, had it been anticipated, might have been managed more effectively and deliberately. Supernant and Warrick (2014) discuss how collaborative archaeology can cause harm when resulting interpretations of the past promote the rights of one/some indigenous communities over others. One thing we must therefore consider explicitly when we approach analyses and interpretations of digital artefacts is the role of amateur enthusiasts in game history and narratives. Judge et al. (2020) discuss how the Western folk theory of artefact creation, which includes lay conceptions of art/craft and industrial production, influences the interpretation and evaluation of artefacts and their makers. We are fortunate in this case that our expert and autoethnographer, Newell, along with his artefacts, gave us unique insight that allowed us to settle the debate about the mysteries of the maze algorithm.

Our assemblage of Entombed materials is curated in that the artefacts we analysed were those that Newell had kept and stored. What is curated illustrates not just the individual choices of the curator, such as what he wanted to keep and could keep, considering factors such as storage space. It also illustrates what can and will be preserved, like the written label in Figure 8 fading over time, and also the larger cultural context: the process of saving files, versions, and determining what hard copies should be kept reflects broader practices in the software development community. For his part, PAN kept what records he felt were necessary to continue working on the maze and, by contrast, he recalls disposing of Towering Inferno material because it was a published game. Upon conclusion of this project, the assemblage is planned to be sent to the National Videogame Museum in Texas.

It is clear that Newell's work on Entombed was early enough in the history of video games that we have a fairly isolated community of designers/developers/programmers; even three years later, there were other trends in video game design, development, and implementation that had taken hold. This means that as Newell was working, he, and other people within the video game development community more broadly, were figuring out the limitations of what could be done and were constantly testing those tangible and intangible boundaries. The platform constraints of the time imposed an 'economy of code' à la archaeology's economy of effort, and we would argue that this is reflected in the simple yet effective Muirhead-Newell algorithm. As the years went on, changes to other parts of the technological system (e.g., hardware), removed many of the constraints forcing conservatism.

However, we also have to consider other constraints that impact technological organisation of early game implementation. Access to tools and knowledge was limited, specialist, and largely untrained (or informally trained) at this time. Video game programming was not something formally taught by experts to novices, and at times knowledge transfer was indirect, and accomplished by reverse engineering others' games. PAN learned on the job and notes that there was a lot of hindsight involved; this is why seeing different versions and even backups is so useful, because we can track not just changes to the game(s) but the process of the maker learning as it occurred. This is not to say that the work being done was by amateurs, but rather of innovative professionals who were applying skills, knowledge, and experience to contribute to the development of an emerging technology.

6. Conclusion

While we have been able to shed light on Entombed's maze algorithm, its backstory, and the development leading up to it, in many ways the larger contribution we are making here is one of process. This study demonstrates the utility of having professionals in several fields working together to address a large number of digital and digital-derived artefacts. Our 487 artefacts pale in comparison with the massive amount of digital heritage that is constantly being generated, of course, yet it still serves as a starting point towards developing processes and procedures. We were fortunate in that Newell's 8-inch floppy disks were readable and that we were able to coax more from them than a cursory examination of the disk directory revealed, but in the long term such feats with old media will become more of a challenge, and archaeology can provide some insight as to how the computing historical record can be approached as we lose this ability. Our work also reinforces some of the basic principles we know about the archaeological record — that it is fragmentary and incomplete no matter the time and/or place we work in.

Working collaboratively on this research with a first-hand participant in the events has been a unique opportunity; Newell has contributed far more than recollections and oral history. Here, we hope that the process we have undertaken to include him and his voice while maintaining objectivity will act as an example for future work. There are doubtless other programmers and designers from this era with these kinds of archives and paper trails; those records would allow other 'deep dives' like this to be undertaken. Organisations such as the Internet Archive, the Strong National Museum of Play, and the National Videogame Museum have been trying to archive what is available from game programmers, designers, and companies — and what archaeology tells us is that these first-hand sources must be used before they are lost.

Acknowledgements

We would like to thank Marlin Eller for access to his notes, and John Hardie, Sean Kelly and Joe Santulli — now running the National Videogame Museum in Frisco, Texas — who dumped the saved EPROMs in May 2003. This article is dedicated to Duncan Muirhead.

The work of the second and third authors is supported by the Government of Canada's New Frontiers in Research Fund (NFRFE-2020-00880).

Appendix 1: Maze Algorithm Example

We illustrate the Muirhead-Newell algorithm by first showing the generation of three consecutive bits, and we have selected the maze context such that all three of the algorithm's rules are applied in this sequence.

In the first step, none of the computed B-KIN or D-KIN values are 0 (the base values are highlighted in bold in the calculations), and neither the sum of B-KIN₀+D-KIN₀ nor B-KIN₁+D-KIN₁ is greater than 4; therefore, Rule 1 and Rule 2 cannot apply. However, the CBLOCK bits are all the same, and Rule 3 applies: because the CBLOCK bits are all 0, the generated bit X is a 1.

For the second step, the computed B-KIN₀ value is 0, thus the generated bit X is again a 1 and the algorithm does not proceed any further. Though not taken into account, Rule 2 would not apply because the sums of B-KIN₀+D-KIN₀ and B-KIN₁+D-KIN₁ are too small, and Rule 3 would not be used as the CBLOCK bits do not all have the same value.

The third step has no computed B-KIN or D-KIN values equal to 0, and Rule 1 does not apply. However, B-KIN₁+D-KIN₁ is greater than 4, so Rule 2 takes precedence and the generated bit is 0. Had the algorithm gone further, the CBLOCK bits are all 1, and Rule 3 would also set X to 0.

Finally, we show a case where none of the three rules applies, and a random bit is generated. No B-KIN or D-KIN values are 0 (Rule 1), no B-KIN or D-KIN sums exceed 4 (Rule 2), and the CBLOCK bits differ (Rule 3).