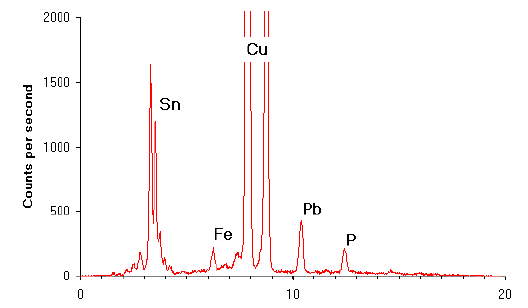
Fig.11 X-ray spectrum produced using EDXRF
This section details the analytical system and sample preparation methods used to obtain the quantitative analyses presented in this article. The analytical instrument used was an energy dispersive X-ray fluoresence (EDXRF) spectrometer. X-ray fluorescence (XRF) is a well-established technique, widely used in industry, which has been used for some time in archaeology for the examination of ancient metals (e.g. Hall 1960; Caple 1986; Cowell 1990). This description of the analytical method concentrates on the practicalities of how EDXRF was used to obtain quantitative analyses of archaeological copper alloys, rather than XRF theory in general. The general theory and principles of XRF can be found in a number of standard reference works (e.g. Williams 1985; Jenkins et al. 1981).
The spectrometer used to obtain the analytical results was fitted with a Rhodium target. This target was excited by a stream of electrons. The target then emitted X-rays with a range of different energies, which were directed on to the sample to be analysed. Incident X-rays could interact with the sample in a variety of ways. For the purposes of EDXRF only one phenomena is of interest - namely fluorescence. Incident X-rays can displace electrons from the inner shells of atoms in the sample, providing they have sufficient energy. The electronic structure of an atom with a displaced inner electron is unstable. In order to achieve a more stable arrangement an outer electron 'falls' from an outer orbit to the inner one. This can occur in a single step, or as a series of steps in those atoms with three or more electron shells. As an electron moves from an outer to an inner shell it emits energy. This is necessary as inner electrons always have less energy than outer ones. The energy which an electron can have in a particular shell is fixed. The energy emitted when an electron 'falls' from an outer shell to an inner shell is the energy difference between the two shells. Thus, whenever an electron moves from a particular outer shell to a particular inner shell in a specified atom the energy emitted is always the same.

Fig.11 X-ray spectrum produced using EDXRF
When excited by X-rays copper always emits X-rays at 8.04 keV. The presence of a range of different elements in a sample produces a spectrum of X-rays with different energies (see Figure 11). The peaks in this spectrum relate to the elements present in the sample. Thus, it is possible to note the presence of many elements from a single analysis. The height of any given peak is proportional to the amount of the element present in the sample. By matching the height of the peak (or for more accuracy the area under the peak) to those derived from the analysis of known standards it is possible to determine the proportion of that element present in the sample.
The EDXRF facility used was a Link Analytical XR200, with the following set up:
Each spectrum was deconvoluted by the dedicated software provided. The output from the attached computer consisted of counts per second (cps) data for a selected peak for each of the elements under consideration. The number of elements that could be sought for in this way was limited to 25 by the software available. The presence of other elements could be visually checked by looking for peaks during spectra collection.
EDXRF spectra will show the presence of any element present in the sample (providing the atomic weight is over 11, that the voltage setting is sufficient to excite all elements, and that the element is present at a sufficient level). Nevertheless, the dedicated software allows the simultaneous detection and measurement of a maximum of 25 elements. The choice of which elements were to be sought was based on what might be expected in the archaeological samples (from previous programmes of work) and the composition of the available standards.
The most important elements sought were the alloying elements zinc, tin and lead. These elements were deliberately added to copper and so reflect the technological, social and economic influences of the period under study. The standards available for calibration were made for use in modern quality control of metal composition and so reflect the alloys presently in use. Archaeological alloys, however, often contain levels of some elements in excess of those found in modern alloys (e.g. speculum, a tin bronze with c.25% tin, used for the manufacture of mirrors in the Roman period. The maximum tin content of modern standards is only c.15%).
The standards also contained low or trace levels of other elements (iron, nickel, manganese, arsenic and antimony). These other elements were also included in the analysis (initially) for the sake of completeness. Elements which were present in the standards and so could be calibrated are shown in Table 3.1.
| Element | Energy of peak used for calibration (keV) |
|---|---|
| Copper | 8.04 |
| Zinc | 8.63 |
| Lead | 10.55 |
| Tin | 3.44 |
| Iron | 6.4 |
| Nickel | 7.47 |
| Manganese | 5.89 |
| Arsenic | 10.53 |
Cobalt was not present in any of the standards available, but previous work (e.g. Northover 1987) suggested that an estimation of cobalt content for Iron Age alloys would be useful. Five samples containing cobalt (which had been used for an inter-laboratory comparison; cobalt content = 0.01%-0.14%) were made available by Peter Northover and Brian Gilmour. These samples were only made available in the latter part of 1993 and so cobalt calibrations were mostly retrospective and were not carried out on Roman samples.
The other elements included in the analysis but not calibrated were gold, silver, aluminium, silicon, phosphorous, sulphur, and chlorine. The first two elements could not be calibrated as no standards containing these elements were available. The other elements were essential for the development of the sample preparation techniques. These elements are present in corrosion layers at moderate levels but are usually below the minimum detectable levels in the actual metal.
The effective penetration of X-rays used in EDXRF is very shallow (typically 10-30 microns) and yet surface corrosion products are regularly in excess of 100 microns thick. Therefore the analysis of an uncleaned archaeological object is essentially an analysis of that object's corrosion products. Table 3.2 shows six analyses taken at different points on the same corroded surface. It can be seen that the analyses of the surface of an object can give widely varying results. (These analyses of corrosion products are not truly representative as the elements are present as oxides, carbonates, etc., and EDXRF cannot detect the presence of the lighter elements, e.g. oxygen and carbon.)
| Cu | Zn | Sn | Pb | Fe | Ca | Si | P | S | |
|---|---|---|---|---|---|---|---|---|---|
| 1st | 85.0 | 1.7 | 0.8 | 0.8 | 1.5 | 0.9 | 7.4 | 1.1 | 0.7 |
| 2nd | 75.0 | 1.2 | 0.0 | 0.7 | 1.6 | 2.3 | 17.3 | 1.8 | 0.0 |
| 3rd | 64.2 | 1.0 | 0.0 | 1.0 | 2.5 | 3.7 | 32.9 | 2.4 | 0.0 |
| 4th | 74.4 | 2.9 | 0.0 | 0.8 | 1.3 | 1.7 | 17.5 | 1.3 | 0.2 |
| 5th | 73.2 | 2.1 | 0.0 | 1.5 | 1.1 | 2.4 | 16.7 | 1.7 | 0.3 |
| 6th | 86.3 | 3.0 | 1.2 | 0.8 | 0.9 | 0.8 | 5.8 | 1.1 | 0.1 |
Analyses of surface corrosion products can be used in a semi-quantitative fashion (Bayley 1983) to confirm the presence of major elements (copper, zinc, tin, lead). For the results to reflect the composition of the alloy accurately, it is necessary to obtain a sample of uncorroded metal. This can be done by cleaning off a sufficient depth and area of corrosion products and so revealing a small patch of uncorroded metal, or by drilling into the object and obtaining drillings of uncorroded metal from the core of the object. The latter method is the only one used in methods which dissolve samples in acid (e.g. Atomic Absorption Spectroscopy) and will be dealt with below. The removal of corrosion products (even from a small area) may be unpalatable to some curators of archaeological material and EDXRF has been used on uncleaned objects to obtain semi-quantitative results (Bayley 1983). EDXRF is also used qualitatively in the routine conservation of objects where the nature of a coating or the object itself may be unclear. Metal cleaning and quantitative analysis has been carried out (e.g. Caple 1986; Cowell 1991) in the past where it has been seen that the information to be gained outweighs the damage to archaeological material. Aesthetic considerations often affect the choices over what damage to an object can and cannot be accepted.
Ancient metal objects are rarely found in pristine condition. Their burial leads to chemical changes, especially at the surface where corrosion products build up. Corrosion begins with the alteration of metal atoms into metal ions which can then react to form corrosion products, i.e.,
M = M+ + e-
This reaction is matched by another reaction which uses up the electrons produced by the metal to metal ion reaction, e.g.,
4e- + O2 + H2O = 4OH-
The amount of energy required to cause ionisation varies for each element.
| Element | Volts (Hydrogen Scale) |
|---|---|
| Au | Au3+ + 3e- +1.50 |
| Ag | Ag+ + e- +0.799 |
| Cu | Cu+ + e- +0.522 |
| Cu | Cu2+ + 2e- +0.337 |
| Pb | Pb2+ + 2e- -0.126 |
| Sn | Sn2+ + 2e- -0.136 |
| Ni | Ni2+ + 2e- -0.250 |
| Fe | Fe2+ + 2e- -0.440 |
| Zn | Zn2+ + 2e- -0.763 |
From this it can be seen that in any given alloy, the metals lower down the scale will be likely to react to form metal ions before metals higher up the scale (less noble elements react before the more noble ones). Thus in a brass, the zinc will react before the copper. In copper alloys in general, the alloying elements react before the copper. This transformation takes place at and near the surface of the metal. The metal ions at the surface will react with available anions. The metal compounds formed have widely varying properties and characteristics which will influence the future corrosion of the metal. Some corrosion products are very soluble (e.g. zinc) and so may be removed completely through the action of ground water. This will lead to a surface depletion of these elements. Where the corrosion products are stable and insoluble, surface enrichment of these elements can take place (e.g. lead).
The properties and characteristics of metals and their corrosion products can vary widely. The surface condition of an archaeological copper alloy object depends on its original composition and the burial circumstances. It is rare for the surface composition of an object to be identical to its core, and it is difficult to predict actual composition from an analysis of the corrosion products.
The quantitative analyses obtained for this thesis were achieved by analysing samples of metal rather than corrosion products. Two methods were used to obtain uncorroded metal for analysis: firstly, abrading/polishing the surface to remove corrosion products; secondly, drilling to remove a sample of metal from the core of the object. The choice of sample preparation method depended on the shape, size and condition of the artefact to be analysed and the wishes of the custodian.
Samples which were to be prepared by abrading/polishing firstly had the corrosion products removed using an air abrasion machine (Cronyn 1990). The surface was then polished using a series of progressively finer silicon-carbide polishing sheets (ending with 6 micron). In order to investigate the degree of abrading/polishing that was required, one sample was progressively ground down and polished. The sample was analysed at each stage until the composition matched that known from the previous analyses. Figure 12 shows the changes in detected alloy composition as the sample was cleaned. As the surface was cleaned the zinc and tin contents increased. The analytical results compare well with conventional understanding of copper corrosion (e.g. Cronyn 1990, 217-219). It can be seen that the composition of the surface of the corroded object is not the same as the composition of the metal itself.
![[Changes in analysed composition as corrosion products are removed]](images/method2.gif)
Fig.12 Changes in analysed composition as corrosion products are removed
In practice, most polished samples were prepared in the following way: a sample was removed from the artefact, all corrosion products were removed using an air abrasion machine, the cleaned sample was then mounted in epoxy resin, finally the mounted sample was polished. The mounted specimens have been retained (except those belonging to the National Museum Scotland which were returned to the museum). These samples are available for further study (e.g. lead isotope, metallography). The polish method was essential for the analysis of any artefacts which were too small to be drilled (e.g. sheet and wire).
The polishing method could not be carried out on many objects as the removal of a fragment was not acceptable, cleaning an area 3-4mm across would be unacceptable, or the artefact was too large to be placed in the EDXRF analysis chamber. In these cases a sample of metal was removed from the core of the artefact using a drill. A portable mini-drill fitted with a 1.1mm diameter Tungsten-carbide drill bit was used to remove 3-5mg of metal from the core of the object. The spot to be drilled was cleaned before-hand to ensure that no corrosion products contaminated the drillings to be analysed.
The drillings were placed in a plastic cup which was fitted with a Mylar film base. The Mylar film is thin enough to have little effect on the X-ray peaks of interest (i.e. 3 keV or more). It was found that the method was accurate and precise to an acceptable degree using as little as 5mg of metal.
The drilled samples were not destroyed during analysis and were retained (except those from the British Museum and the National Museum of Scotland which were returned).
The percentage of each element present in a sample is proportional to the area under the peak measured in counts per second (cps). The cps results can be converted into percentages by comparison with standards (calibrated). The range of elements present in each of the standards used for the calibration is shown in Table 3.4. The composition of these modern standards reflects contemporary metallurgical needs. The majority of these alloys are brasses or gunmetals. Even those alloys which are bronzes tend to have at least some zinc present. Zinc is added to most modern alloys to act as an anti-oxidant. Many prehistoric alloys, however, have no detectable zinc. Even more problematic are those elements whose range falls short of the range found in archaeological alloys. The maximum tin content found in Roman alloys is around 26% (in speculum bronze used for mirrors). The maximum tin content in the available standards falls considerably short of this. The Ancient Monuments Laboratory (through Justine Bayley) kindly provided a sample of a high tin bronze (tin = 24%) which was used to examine the extrapolation of the calibration function (see below). The maximum lead content found in archaeological alloys far exceeds that found in the calibration standards (some Roman alloys appear to contain 40% or more lead). The maximum levels of nickel, iron and manganese in archaeological alloys are usually below the maximum levels in the calibration standards. The maximum arsenic levels in archaeological alloys, however, usually exceeds those found in the standards.
| Standard | Cu | Zn | Sn | Pb | Fe | Ni | As | Mn |
|---|---|---|---|---|---|---|---|---|
| NBS 1103 | 59.27 | 35.72 | 0.88 | 3.73 | 0.26 | 0.15 | 0.00 | 0.00 |
| NBS 1109 | 82.20 | 17.40 | 0.10 | 0.07 | 0.05 | 0.10 | 0.00 | 0.00 |
| NBS 1111 | 87.10 | 12.80 | 0.02 | 0.02 | 0.01 | 0.02 | 0.00 | 0.00 |
| NBS 1116 | 90.30 | 9.40 | 0.04 | 0.04 | 0.05 | 0.05 | 0.00 | 0.00 |
| NBS 1118 | 75.10 | 21.90 | 0.00 | 0.02 | 0.06 | 0.00 | 0.01 | 0.00 |
| C42x01 | 66.00 | 32.52 | 0.83 | 0.12 | 0.19 | 0.10 | 0.05 | 0.11 |
| C71x11 | 82.88 | 6.00 | 5.90 | 4.00 | 0.12 | 0.54 | 0.19 | 0.06 |
| C71x21 | 83.56 | 4.90 | 5.20 | 5.30 | 0.00 | 1.00 | 0.00 | 0.00 |
| C50x31 | 75.75 | 0.57 | 9.60 | 11.10 | 0.25 | 1.60 | 0.14 | 0.02 |
| C50x34 | 77.59 | 1.00 | 11.60 | 8.20 | 0.17 | 0.72 | 0.08 | 0.19 |
| C30.05 | 70.10 | 29.90 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| C52.05 | 60.46 | 39.54 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| C52.21 | 59.69 | 35.64 | 1.54 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| C50.01 | 76.17 | 0.63 | 9.20 | 10.70 | 0.06 | 2.00 | 0.20 | 0.04 |
| C42.23 | 74.50 | 22.39 | 1.40 | 0.55 | 0.32 | 0.13 | 0.17 | 0.01 |
| C54.06 | 84.72 | 0.19 | 12.70 | 0.16 | 0.18 | 0.80 | 0.02 | 0.16 |
| C51.13 | 89.44 | 0.33 | 0.19 | 0.07 | 1.90 | 0.02 | 0.23 | 0.79 |
| C51.14 | 89.29 | 0.56 | 0.08 | 0.00 | 0.73 | 0.20 | 0.36 | 0.52 |
| NIGEL | 89.00 | 5.20 | 3.36 | 1.01 | 0.30 | 0.19 | 0.64 | 0.00 |
The calibration functions for each element were calculated using SPSS. In most cases the function was a simple linear relationship (Figure 13), in others the linear relationship was influenced by another element. This problem usually arose where the peaks used for calibration overlapped (e.g. antimony and tin). The formulas used for calibration are shown in Table 3.5.
![[Relationship between zinc content and measured cps for standards]](images/method3.gif)
Fig.13 Relationship between zinc content and measured cps for standards
| Element | Polished method | Drilled method |
|---|---|---|
| Zinc | Zn.cps*0.01966 + 0.016 | Zn.cps*0.02217 + 0.0016 |
| Tin | Sn.cps*0.03887 + 0.0129 | Sn.cps*0.06725 + 0.0137 |
| Lead | Pb.cps*0.07339 + 0.0487 | Pb.cps*0.08047 + 0.0112 |
| Iron | Fe.cps*0.005981 - 0.0404 | Fe.cps*0.008548 - 0.0497 |
| Nickel | Ni.cps*0.009556 - 0.0653 | Ni.cps*0.01419 - 0.0474 |
| Arsenic | As.cps*0.03409 + Pb.cps*0.00103 - 0.0024 | As.cps*0.05851 + Pb.cps*0.00124 - 0.0176 |
| Manganese | Mn.cps*0.006631 - 0.0031 | Mn.cps*0.00977 - 0.00485 |
| Cobalt | Co.cps*0.005778 + 0.0048 | Co.cps*0.009284 - 0.0061 |
The nature of the sampling methods necessitated the normalisation of raw cps prior to calibration. The size of polished samples varied somewhat (some, such as wire, were smaller than the area usually excited by the X-ray beam, others, such as sheet, were thinner than the depth usually penetrated by X-rays). In addition the weight of drillings varied from sample to sample. In order to ensure that all samples were quantified in the same way the total raw cps data for each sample were normalised (to 7000 cps for polished samples, to 5000 cps for drilled samples) prior to calibration.
The calculation of regression equations for copper presented a number of difficulties. The 'best fit' equation involved the use of four factors (the cps data for copper, zinc, tin and lead). This procedure worked well for samples with low or moderate levels of alloying elements but was much less satisfactory where alloy element content was high (the errors from each different element would be combined). A more reliable calculation of copper content was by difference (i.e. 100% - sum of all other elements). This procedure is reliable here as corroded samples have not been included and the raw cps data were normalised prior to calibration.
The collection of counts per second data for each peak and its calibration was repeated for the full range of standards. Each standard was prepared in both of the ways used for analysis: as a solid polished sample, and as 5mg of drillings. This was necessary as spectra were collected from samples using both of the methods.
A number of different methods were used to estimate the minimum detectable levels (MDL) of the elements sought. One method involved estimating the variation in the background around a peak and relating this to the calibration function for that element. This method tends to underestimate the minimum detectable levels of the elements sought. Most element peaks overlap to a certain extent and this introduces extra variation in the background. In addition, calculating the variation in the background is difficult as the background radiation is not uniform - the absorption edge of each element will give rise to a variation in the background on the low energy side of each peak (Statham 1977). A second method used the data supplied by the EDXRF spectrometer. Each result is accompanied by a relative standard deviation (RSD) figure based on the internal estimation of the variation in the background either side of the peak in question. The RSD is inversely proportional to the amount of the element present. The MDL can be estimated by plotting the RSD against known percentage of element. The MDL occurs when RSD equals 50%. A third method of estimating the MDL makes use of the fact that some elements are not present in all the standards. At any percentage level the measured cps varies. By measuring the variation in the cps of an element at 0% it is possible to estimate the MDL. All three methods were in approximate agreement but the highest estimates for each element were used as MDL for this report. The estimates of MDL were similar for both polished and drilled methods.
| ELEMENT | Minimum Detectable Level |
|---|---|
| Zinc | 0.10% |
| Lead | 0.15% |
| Tin | 0.10% |
| Iron | 0.04% |
| Nickel | 0.05% |
| Manganese | 0.01% |
| Arsenic | 0.10% |
The EDXRF analysis of archaeological samples will be subject to a wide range of errors (the most important of which are 'noise' and errors in fitting the calibration data to a function). Errors in analytical techniques in archaeological science are rarely dealt with at any length. This section contains some attempts to calculate the confidence limits for the analytical results presented in this article.
The regression equations used to calculate the composition took the form:-
![[Equation 1]](./images/equatn1.gif)
![[Equation 2]](./images/equatn2.gif)
The Standard Error can easily be calculated and is regularly provided by statistical computer applications (see Shennan 1988: 136 for a discussion). The Standard Error is usually the largest contributor to the estimated error limits in this case but it is constant. The total error for the regression should be at a minimum at the centre of the known compositions and increase as the regression is extrapolated.
The error in the regression analysis at any one point can be estimated using a matrix calculation of the variance (Var) and co-variance (Cov) values from the regression analysis. The variance is the square of the standard deviation, the co-variance is the product of two factors standard deviations and their correlation coefficient (see Blalock 1972: chapters 16 and 17).
![[Equation 4]](./images/equatn3.gif)
This function provides an additional error for the regression
analysis. 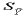 is very small near the centre of the known
compositions but increases geometrically as the regression is
extrapolated.
is very small near the centre of the known
compositions but increases geometrically as the regression is
extrapolated.
The two terms  and
and
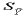 provide estimates of the accuracy
of the regression equations used for this article, but the additional
factor
provide estimates of the accuracy
of the regression equations used for this article, but the additional
factor 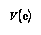 has to be considered. This is the variance of
any single reading. This factor has to be included as the regression
equations were based on repeat analyses of standards but the unknowns
were based on single determinations. The repeat analyses of the
standards does, however, provide an indication of the relationship
between the variance of individual readings and the level of the
element present (Figure 14 shows this relationship
for lead). The relationship between the variance and the level
of each element was estimated using a least squares fit. The slope
and intercept for each element varies (but in all cases these
were positive).
has to be considered. This is the variance of
any single reading. This factor has to be included as the regression
equations were based on repeat analyses of standards but the unknowns
were based on single determinations. The repeat analyses of the
standards does, however, provide an indication of the relationship
between the variance of individual readings and the level of the
element present (Figure 14 shows this relationship
for lead). The relationship between the variance and the level
of each element was estimated using a least squares fit. The slope
and intercept for each element varies (but in all cases these
were positive).
![[Variance of lead determinations for the standards]](images/method4.gif)
Fig.14 Variance of lead determinations for the standards
These estimates were then used to calculate 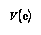
![[Equation 5]](./images/equatn4.gif)
The use of the above three estimates of error provides a total error estimate which should provide confidence limits for the results used in this article (including those results which lie outside the range of compositions of the standards). Figure 15 shows the changes in error estimate with composition for zinc. It can be seen that the estimated error is low for low zinc contents but increases as zinc content increases.
![[Error estimate for zinc]](images/method5.gif)
Fig.15 Error estimate for zinc
EDXRF has been used to analyse the copper alloy samples for this article. As EDXRF is essentially a 'surface' analysis method, the samples were prepared by polishing or drilling. The raw cps for each sample were converted into percentages by comparison with standards of known composition.
The method of estimating the errors associated with the use of regression analysis in predicting the composition of unknown samples starts with the Standard Error but also includes two extra factors: one which reflects the varying accuracy of the regression analysis at different points along the regression function, and a second which estimates the uncertainty involved in taking any one single EDXRF measurement. This method was applied to each of the elements reported in this article (except copper and cobalt). A summary of these results is shown in Table 3.7
| ELEMENT | one sd (65% probability) | two sd (95% probability) |
|---|---|---|
| Zinc | +/- 0.45% | +/- 0.90% |
| Tin | (0-15%) | +/- 0.35% +/- 0.7% |
| Tin | (15-30%) | +/- 0.4% +/- 0.8% |
| Lead | (0-10%) | +/- 0.5% +/- 1.0% |
| Lead | (10-15%) | +/- 0.6% +/- 1.2% |
| Lead | (15% +) more than | +/- 0.6% more than +/- 1.2% |
| Iron | +/- 0.02% | +/- 0.04% |
| Nickel | +/- 0.06% | +/- 0.12% |
| Manganese | +/- 0.02% | +/- 0.04% |
| Arsenic | +/- 0.36% | +/- 0.72% |
©
Internet Archaeology
Last updated: Thu Apr 3 1997