Internet Archaeol. 13 Christen Technical Wiggle matching

The theory of Bayesian wiggle-matching has been developed in full in Christen and Litton (1995), and in general, the theory of Bayesian Calibration has been developed in Buck et al. (1991); (1992); Christen (1994a); Christen and Buck (1998); Buck and Christen (1998), Gomez-Portugal Aguilar et al. (2002); Nicholls and Jones (2001), among others. Here the theory of wiggle matching is briefly presented, plus a further consideration to deal with outliers.

Let y = (y₁, y₂, y_m) be a series of radiocarbon determinations with their corresponding standard errors σ₁, σ₂, ... ,σ_m, and their associated calendar ages θ = (θ₁, θ₂, ... , θ_m) (that is, the calendar ages at which each sample radiocarbon dated ceased metabolising). The output of a radiocarbon analysis, as provided by the laboratory, is an estimated date in the radiocarbon scale (y_j) and a standard error (σ_j). The standard error reported is calculated using both empirical and theoretical considerations and the usual assumption is to consider it as known (see below). Here, we assume that θ_i - θ_j it is known exactly; most likely the radiocarbon dated samples were taken from chunks of tree-rings in a log or timber. The model we use is the following

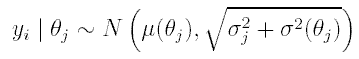
$LaTex math formula: $$ y_i \mid \theta_j \sim N\left( \mu(\theta_j), \sqrt{\sigma^2_j + \sigma^2(\theta_j)}\right), $$$

where μ (θ_j) is the piece-wise linear calibration curve (we are using the INTCAL98 calibration curve, see Stuiver et al. 1998) and σ²(θ_j) is a variance term arising from the errors observed in the calibration curve (see Christen and Litton 1995 and Christen 1994a). We also assume that ƒ(y | θ) = π ^m_j=i ƒ(y_i | θ_j) (conditional independence). That is, σ_j is assumed known, which is the usual assumption in radiocarbon dating, and the determinations are considered as conditional independent.

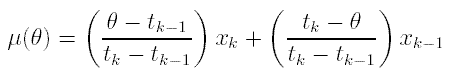
$LaTex math formula: $$ \mu(\theta) = \left(\frac{\theta - t_{k-1}}{t_k - t_{k-1}}\right)x_k + \left(\frac{t_k - \theta}{t_k - t_{k-1}}\right)x_{k-1} $$$

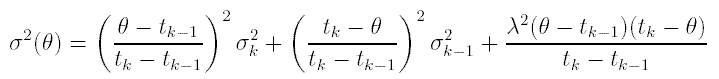
$LaTex math formula: $$ \sigma^2(\theta) = \left(\frac{\theta - t_{k-1}}{t_k - t_{k-1}}\right)^2\sigma^2_k + \left(\frac{t_k - \theta}{t_k - t_{k-1}}\right)^2\sigma^2_{k-1} + \frac{\lambda^2 (\theta - t_{k-1})(t_k - \theta)}{t_k - t_{k-1}}, $$$

for t_k > θ >= t_k-1; where t_k ± σ_k is the pooled radiocarbon determination for the calibration curve at knot (calendar year) x_k. λ is taken to be 19 (see Christen and Litton 1995 and Christen 1994a), although Gomez-Portugal Aguilar et al. (2000) argue that a lower value could be used.

The definition of σ ²(θ) is based on a Brownian bridge model (see Billingsley 1999, 93) and represents a simple, although realistic, way to include the errors in the calibration curve (see Christen and Litton 1995; Christen 1994a; Gomez-Portugal Aguilar et al. 2002 and Nicholls and Christen 2000 for a more in-depth discussion). The option where no errors are included in the curve is covered simply by fixing σ ²(θ) = 0.

In many applications, and for practical reasons, the inclusion of the errors in the calibration curve is neglected. This is in fact good practice, as the variance in the posterior is comparatively higher than the variances in the curve. This is normally not the case in wiggle-matching because of the increased precision arising from the simultaneous calibration of several radiocarbon dates, even if the individual standard errors are big.

Let us assume that θ₁ <= θ₂ <= ... θ_m and that θ₀ is the (unknown) calendar date for the event to be dated (this event may or may not coincide with any of the θ_j). We assume that θ_j = θ₀ + α_j where, as mentioned above, α_j is known exactly (α_j could be negative). The only unknown parameter then is θ₀ and its posterior density is given by

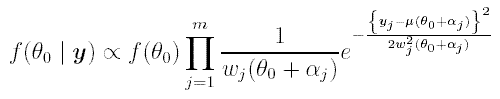
$LaTex math formula: $$ f( \theta_0 \mid \vy ) \propto f(\theta_0) \prod_{j=1}^m \frac{1}{w_j(\theta_0 + \alpha_j)} e^{-\frac{\left\{y_j - \mu (\theta_0 + \alpha_j)\right\}^2} {2w_j^2(\theta_0 + \alpha_j)}} $$$

where w_j² (θ) = σ_j² + σ ²(θ). The prior f(θ₀) is an uniform distribution provided by the user (upper and lower bounds for θ₀). This posterior is normalised numerically and provided as a histogram, both with (see Figure 2) and without (see Figure 1) considering the errors in the calibration curve. (Unfortunately Bwigg only allows for uniform priors, although mexcal could be used directly to consider more sophisticated priors. This feature is not yet included in Bwigg.)

Outliers

The analysis of 'shift outliers' is based on Christen (1994b). A shift in the radiocarbon scale δ_j is considered for each determination, having a priori distribution

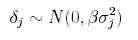
$LaTex math formula: $$ \delta_j \sim N( 0, \beta \sigma_j^2) $$$

We fix β = 2. The latent variable Φ_j = 0,1 is also introduced. If y_j is an outlier then Φ_j = 1, and thus needs a shift δ_j in the radiocarbon scale to be corrected. The following model [2] is assumed:

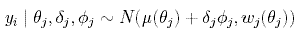
$LaTex math formula: $$ y_i \mid \theta_j,\delta_j, \phi_j \sim N( \mu(\theta_j) + \delta_j \phi_j, w_j(\theta_j)) $$$

Interest then focuses on approximating P(Φ_j = 1 | y), the posterior probability of determination j being an outlier. MCMC is used to approximate P(Φ_j = 1 | y). In turn, a simulation is run from the full conditionals of each of the Φ_j's (Bernoulli distributions) and δ_j's (normal distributions, see Christen 1994b). To simulate from θ₀, a proposal is simulated θ₀' form f(θ₀) and accept it with probability

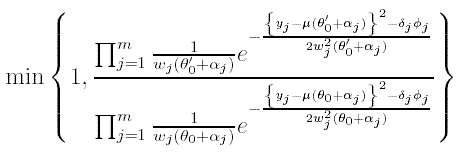
$LaTex math formula: $$ \min \left\{ 1, \frac { \prod_{j=1}^m \frac{1}{w_j(\theta_0' + \alpha_j)} e^{-\frac{\left\{y_j - \mu (\theta_0' + \alpha_j)\right\}^2 - \delta_j \phi_j} {2w_j^2(\theta_0' + \alpha_j)}} } { \prod_{j=1}^m \frac{1}{w_j(\theta_0 + \alpha_j)} e^{-\frac{\left\{y_j - \mu (\theta_0 + \alpha_j)\right\}^2 - \delta_j \phi_j} {2w_j^2(\theta_0 + \alpha_j)}} } \right\} $$$

The resulting MCMC is very well behaved in that the support of f(θ₀) is not too wide in comparison to the main bulk of the posterior for θ₀. 10,000 samples are taken, every 10 passes, with a burn-in of 1,000 passes. This is usually enough for approximating P(Φ_j = 1 | y).

Footnote 2: Note that the errors in the calibration curve are taken into consideration via w_j(θ_j)

4 Bayesian wiggle-matching (technical)

This section is intended for statisticians.

Outliers