The relational model, first described by Codd (1970), provides a simple and elegant means of describing and manipulating data. Its theoretical basis lies in the mathematical concepts of sets and relations (Fig. 1). A relation (informally referred to as a table) is a set of tuples (informally, rows) with the following characteristics:
Because the rows of a table form a set, each row is unique and can be distinguished from all others simply by the values of its attributes. In practice, several combinations of one or more attributes may serve as a unique identifier for a row, and one of these is chosen to act as the identifier, or primary key. Whilst the values of non-key attributes may be empty, or null, those of the primary key must always be present in order to ensure that each row may be uniquely identified, and so distinguished from all others in the table.
| Attribute1 | Attribute2 | Attribute3 | |
| Tuples/rows | 1 | this | 95 |
| 2 | that | NULL VALUE | |
| 3 | the other | 66 | |
|
Primary Key Unique Values |
Non-key Not unique |
Non-key, may include NULLS |
Figure 1: The components of a relation (table)
Each row of a table represents a single instance of some recorded entity. Relationships between such instances are also expressed by values stored in columns (Fig. 2). To express a relationship, foreign key columns are added to one table and are used to hold the value of the primary key of the related instance. The values stored in these foreign key columns must either equate to an existing primary key in the related table, or be wholly null, the latter implying that the row is not related to one in the related table. In Figure 2, the foreign key of find 1023 is null, indicating that the find is not associated with any layer, a convention that might usefully be adopted to indicate unstratified material.
| LAYERS | FINDS | |||||||||
| ID | Description… | … | ID | Type | ... | Layer | ||||
| 123 | Pit fill | … | 1022 | Pot | … | 123 | ||||
| 124 | Stake hole fill | … | 1023 | Pot | … | NULL | ||||
| 125 | Pit fill | … | 1024 | Coin | … | 123 | ||||
| … | … | … | 1025 | Tile | … | 125 | ||||
| … | … | … | … | … | … | … | ||||
Figure 2: Relationships between relations (tables). The Layer attribute in the FINDS table acts as a foreign key to the LAYERS table
Because all values must be atomic, the foreign key values in any row can relate to only one row in the other table. However, the same foreign key values may occur in many different rows. For example, in Figure 2, there are two finds (1022 and 1024) related to layer 123. Thus, this method provides a straightforward means of expressing both one-to-one (1:1) and one-to-many (1:n) relationships. Many-to-many (m:n) relationships can only be expressed by adding a link or intersection table. This table contains only foreign keys, one for each of the two related tables, and exists solely to represent the relationship. Examples of this appear below in Figure 4.
The simplicity of the relational model is achieved by breaking down a complex data structure into its simplest components. Meaningful information retrieval invariably involves the re-combination of these components to form the required results. Set theoretic operations such as union, intersection or difference may be applied to pairs of similarly structured relations. Additionally, specifically relational operators may be used to extract specified columns or rows from a single relation, or to join two relations according to some condition (typically the equality of values between the primary key of one relation and a foreign key in the other). The result of applying any of these operators is a new relation or table.1 Fortunately for the relational DBMS user, the complexity of assembling meaningful queries out of such low-level operations is at least partly simplified by languages such as SQL and other query interfaces provided by the DBMS.
The SQL language provides statements to create tables with appropriate constraints to comply with the theoretical model (uniqueness of primary keys, validity of foreign keys, etc.), as well as a full range of data input, update and retrieval statements to operate on existing tables. In addition, most systems also support statements for improving performance by, for example, creating indexes on particular columns, and for maintaining security by controlling user access to data.
Relational database design centres on modelling a collection of data in terms of entities, attributes and relationships. The most widely used techniques are based on the Entity-Relationship (ER) model originally described by Chen (1976). An entity (strictly an entity class) represents a class of physical or conceptual objects with shared characteristics (attributes) about which data must be recorded. In an ER diagram (Fig. 3) these are usually represented as named boxes, with the relationships between them indicated by lines. Many different notations are used for the relationships: solid lines may indicate a mandatory relationship whilst dotted or dashed lines may be used to indicate that its existence is optional. A 'crow's foot' at one end is usually employed to indicate the 'many' end of a 1:n or m:n relationship.
Attributes may also be shown on an ER diagram although they are often
omitted in order to minimise complexity. Again, several different
notations are in common use. One of these, where they may appear
listed beneath the entity name, is shown in Figure 3.
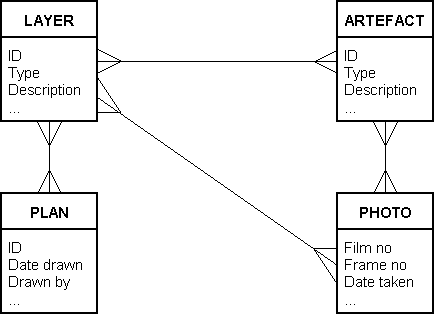
Figure 3: A simple Entity-Relationship (ER) diagram representing part of the design for an excavation database
There is a very close correspondence between the abstract model in an ER diagram and an implementation using a relational DBMS. Entity classes map directly to tables, to which foreign key columns must then be added to implement the relationships. Where the ER model shows a m:n relationship, additional link tables must also be created. In the case of the ER diagram in Figure 3, four base tables Layer, Artefact, Plan and Photo would be created and the LayerID column added as a foreign key in the Artefact table. Then three link tables LayerPlan, LayerPhoto and ArtefactPhoto would be needed to represent the m:n relationships. Each of these contains only the foreign keys necessary to link to the related tables. For example, the link table LayerPlan has LayerID as the foreign key to Layer, and PlanID as the foreign key to Plan. For each of these link tables, the primary key is the composite of both foreign keys. These are shown in Figure 4.
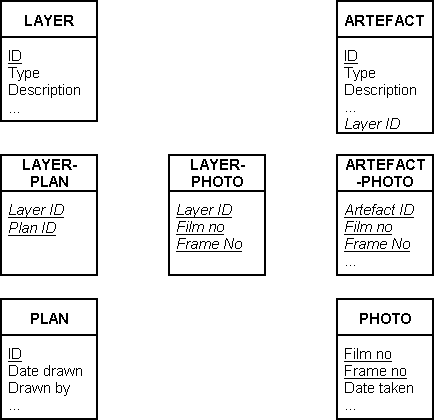
Figure 4: A relational database implementation of the ER diagram in Figure 3. Primary keys are shown underlined, foreign keys in italic
© Internet Archaeology
URL: http://intarch.ac.uk/journal/issue15/8/nr3.html
Last updated: Wed 28 Jan 2004