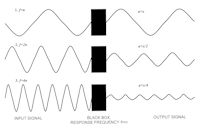
Figure 1: The 'Black Box'. Input signals (left) produce output signals (right) of increasingly low amplitude (a) as input frequency (f) increases beyond the response frequency (fr) of the 'Black Box' coupling mechanism.
Hierarchy theory is a wide-ranging body of concepts with a long history derived from general systems theory and concerned with understanding and analysing systems organised on multiple scales (Grene 1969; papers in Pattee 1973). Most real-world systems are so organised, and hierarchy theory has consequently been influential in a range of disciplines. It is particularly important in ecology (e.g. Allen et al. 1984; O'Neill et al. 1986; Dooley and Bowers 1998; Parsons et al. 2004; Fisher et al. 2006; Sheldon 2008; Morin 2011) but also has applications in physiology (e.g. Henzler-Wildman et al. 2007) and in interdisciplinary approaches that seek to unify the life and social sciences (e.g. Warren 2005; Allen et al. 2009). A hierarchical approach can therefore illuminate the modernity problem if it is understood in terms of the dynamics of a multi-scale modern knowledge system.
The hierarchical approach to system organisation can be understood by analogy with a series of photographs of increasing magnification taken by a powerful zoom camera from an orbiting satellite (Forman 1995, 11-12). One can begin with a view of the planet, and then focus in turn on continents, regions, localities and on until soil particles are visible. With increasing magnification, elements visible at lower resolutions disappear from view and whole new complexes of elements, previously invisible, become apparent. In this analogy, scale domains represent orders of magnitude of size, and thus of perceptibility at particular resolutions of observation. While real-world systems, including human knowledge systems in the palaeolithic, certainly exhibit scalar organisation in space, the key system property that the zoom camera analogy illustrates is the scalar distribution of process rates.
System components interact through processes of causal relationships such that events or perturbations in one component will cause responses in other system components. But processes of interaction between system components do not all proceed at the same rate. According to Simon, it is precisely because different system processes operate at very different rates that systems resolve into scale domains (Simon 1962; 1969; 1973). A relationship between two system components, in which a change or perturbation in one causes a change or perturbation in the other, can be represented in terms of an input signal inducing an output signal. The process mechanism that links these two components in their causal relationship can in turn be thought of as a black box (O'Neill et al. 1986, 77; King 1996). Black boxes operate at characteristic rates or frequencies, which specify a characteristic response time (the time it takes to respond to an input signal). Consequently the black box's capacity to transmit an input signal to an affected component and induce an output signal response is conditioned by the relationship between its own characteristic operating rate or frequency (and therefore its response time), and the rate or frequency of the input signal (Figure 1).

Figure 1: The 'Black Box'. Input signals (left) produce output signals (right) of increasingly low amplitude (a) as input frequency (f) increases beyond the response frequency (fr) of the 'Black Box' coupling mechanism.
An example of this in ecology is Woodward's exploration of the response of plant organs to the daily cycle of external temperature change. The organ's response time, which increases with its thickness, is the time taken for its centre to equalise with the external temperature following a change in the latter. Recording of centre temperatures over a period of five days in organs with response times of 1 hour, 6 hours and 24 hours demonstrated that, given an identical external temperature history (the input signal), the different response times mediated quite different responses (output signals). Organs with a response time of 1 hour (a thick broad leaf) responded to, or 'perceived', all of a 20°C daily range in air temperature. Thicker organs with a response time of 6 hours subjected to the same 20° daily temperature range experienced or perceived a temperature range of only 12°C at their centres; that is, the output signal was damped or attenuated relative to the input signal. Finally, when the organ had a response time of 24 hours (a stem with a diameter of 30cm), the temperature curve at its centre had an amplitude of only 4°C (Woodward 1987, fig. 2.6). This illustrates how an increase in the process rate or frequency of a black box linking mechanism (i.e. a reduction in its response time) will lead to a responding system component becoming more sensitive to stimulus by causal factors. Woodward concludes (1987, 21) that, broadly, causal/input signals whose frequency is at least ten times lower than that of the black box linking mechanisms' response frequency will induce response/output signals exhibiting scarcely any amplitude loss, while causal/input signals whose frequency is at least ten times higher than the black box response frequency will be so heavily damped or attenuated as to stimulate little or no output response (see Figure 1).
This example shows how, within systems, inputs from high frequency or high process-rate components generally have limited or even no effect on lower frequency, lower process-rate components. Systems consequently exhibit organisation into vertical arrays or hierarchies of process-rate levels or scale domains. Each level in the hierarchy acts as a filter, attenuating the impact of relatively rapid, high-process rate and short time scale dynamics on levels characterised by lower process-rate interactions operating on longer time scales. High process-rate dynamics are therefore restricted to 'lower' levels in the hierarchy; this has been termed 'loose vertical coupling' (Simon 1973). On the other hand, the effects of low frequency dynamics operating at low process rates and long time scales will be felt in full across the system since black box linking mechanisms respond to input signals with frequencies much lower than their own with little or no attenuation. System hierarchies can therefore be understood in terms of low hierarchical levels characterised by high process-rate dynamics, and high levels at which low process-rate dynamics operate. While the system impact of rapid low-level dynamics diminishes as one ascends the hierarchy, lower process-rate dynamics at high hierarchical levels will have effects at all lower levels (Figure 2).
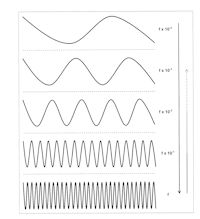
Figure 2: Process rates and system hierarchy. System processes are here represented by sine curves of different frequencies (f). Low frequency dynamics exert causal effects on dynamics operating at all higher frequencies (downward arrow).The impact of high frequency dynamics on lower dynamics is limited by the capacity of low frequency 'black box' linking mechanisms to transmit them. Consequently systems resolve into process rate hierarchical levels, and the effect of high frequency processes is progressively damped as one 'ascends' the system (upward arrow).
Signal transmission between higher and lower levels within a system is therefore vertically asymmetrical. It is important to emphasise here that, although high levels in the system hierarchy do not respond to dynamics operating a low levels, it does not follow that low-level processes are insignificant at higher levels. Low level, high process-rate dynamics deliver a signal to higher hierarchical levels, but that signal becomes progressively more attenuated, integrated and averaged as it percolates up the system hierarchy. At high hierarchical levels, low level processes, while operating too rapidly for their dynamics to be perceived, will constitute a static boundary condition (Figure 3). Indeed, Grene (1969) has argued that hierarchical system organisation involves a double asymmetry in that low level dynamics are essential to the functioning and persistence of higher level processes, but these in turn constrain flexibility and response range at lower levels. High and low hierarchical levels within a system are, from that standpoint, interdependent and mutually reproducing.
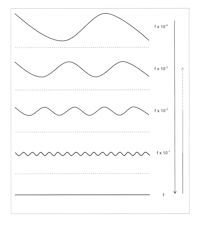
Figure 3: Vertical asymmetry. Because high level, low-frequency dynamics (here shown at the top of the hierarchy with a notional process rate of fx10-4) are progressively less sensitive to the effects of higher frequency processes, then as one descends the hierarchy towards increasingly high-frequency processes, a level is reached at which processes operate so rapidly that they are invisible at the high, low process rate level and instead present as a static boundary condition.
All systems can be regarded as being organised on scales from the vanishingly short and sub-atomic to the cosmic. Within that vast scale range dynamic interactions can only be identified as high or low process-rate relative to a particular hierarchical level or scale domain. Any particular level in a hierarchy can be regarded as a high level constraint in relation to much lower levels and, at the same time, as a static boundary condition relative to dynamics taking place at much higher levels. And just as, from the perspective of a particular level in the hierarchy and its characteristic time scales, rapid processes at much lower levels are integrated and averaged to the point at which they come to constitute a static boundary condition, then similarly processes at much higher levels operate so slowly that they effectively become a static constraining constant. The hierarchical scalar 'distance' one must travel in both 'directions' from a specified level in a system hierarchy before one reaches an upper 'ceiling' of non-dynamic constraint in one direction and a lower 'floor' or static boundary condition in the other can be referred to as the dynamic scale range characteristic of the system component or process under investigation (Figure 4). Processes at scales outside the dynamic scale range will be invisible to the specified component or process and will exert no effect on it over the time scales on which it operates (Hopkinson 2007, 16).
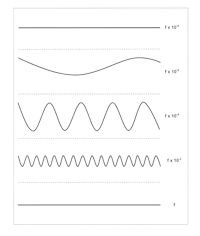
Figure 4: Double asymmetry and the dynamic scale range. From the perspective of processes at a particular hierarchical level (shown here in the centre of the hierarchy with a notional process rate of fx10-4), static boundary conditions occur both at a lower 'floor' (double asymmetry) and at a higher 'ceiling', at which dynamics operate so slowly as to be imperceptible. The scale distance between the lower static floor and the upper static ceiling, within which processes are mutually sensitive, can be termed the dynamic scale range.
Of course, real world systems are complex, their boundaries (and thus their components) are problematic (O'Neill et al. 1986), and they are rarely in equilibrium or steady-state (Connell and Sousa 1983; Lloyd and Stupfel 1991). While high and low level processes and dynamics within a system might be mutually reproducing, catastrophic transformations in either or both can result in a radical restructuring of the system, or even its collapse. However, the crucial issues of relevance here are:
Internet Archaeology is an open access journal based in the Department of Archaeology, University of York. Except where otherwise noted, content from this work may be used under the terms of the Creative Commons Attribution 3.0 (CC BY) Unported licence, which permits unrestricted use, distribution, and reproduction in any medium, provided that attribution to the author(s), the title of the work, the Internet Archaeology journal and the relevant URL/DOI are given.
Terms and Conditions | Legal Statements | Privacy Policy | Cookies Policy | Citing Internet Archaeology
Internet Archaeology content is preserved for the long term with the Archaeology Data Service. Help sustain and support open access publication by donating to our Open Access Archaeology Fund.
File last updated: Mon June 10 2013